Crossword Science with Stan
One of the biggest Slack channels at UW is called #minicrossword: it
is a channel for fans of the NYT Minicrossword to post their times.
Times are recorded by a Slack bot that Max wrote, so that we can crown
a daily winner, improve over time, or try to beat our nemeses. But one
scary truth is that some people solve crosswords better than others;
so some people win almost every day while others are nearly always at
the bottom of the standings.
I wanted to fix this, and thought it would be neat to do that by predicting people's times for each crossword, and then congratulating people who do much better than predicted. If the predictions are good, your innate skill at crossword won't affect your place in the rankings much.
Modeling the Crossword data
I started by downloading all of the times anyone had ever posted in the channel; in total, there were about eight thousand submissions, covering almost 500 crosswords. Since each submission was defined by a player and a date, I figured that the simplest model would have a per-crossword difficulty and a per-player skill, and the two of those would predict the time.
Since I've been reading Andrew Gelman's blog for years, I figured this was a good opportunity to learn Stan, and in fact, Stan made it pretty easy to set up this model. I created three array's worth of data: one for the submitted times, one for the user that did the submitting, and one for the date they were submitting for. In Stan, you can write that like this:
data {
int<lower=0> Ss; // number of submissions
int<lower=0> Us; // number of users
int<lower=0> Ds; // number of dates
real secs[Ss];
int<lower=1,upper=Us> uids[Ss];
int<lower=1,upper=Ds> dates[Ss];
}
Note that the users and the dates are integers from 1 up to some bound. This is because Stan's only data types are integers and reals, and arrays of both.1 [1 It also has matrices and vectors, but I don't know how they differ from arrays of reals.] I make the users and dates count from 1 because I want them to be array indices, and in Stan arrays start at 1.
Now, the great thing about Stan is that you can just freely define your model. Here, I wanted to have a per-user skill parameter and a per-date difficulty parameter:
parameters {
vector[Us] skill_effect;
vector[Ds] difficulty_effect;
...
}
However, I also need a few other parameters to make this work. I wanted skills and difficulties to be normalized to 0, so to do that I'd need to subtract out the average time. And skills and difficulties would have to be drawn from some distribution—normal seemed like a good assumption—so I'd need to define parameters for that distribution:
parameters {
...
real<lower=0> mu; // average time
real<lower=0> sigma; // size of errors in prediction
real<lower=0> skill_dev; // st. dev. of skills
real<lower=0> difficulty_dev; // st. dev. of difficulties
}
I already knew (from plotting the data) that crossword times are log-normal,2 [2 The fastest time in the dataset is six seconds, and the slowest about nine minutes.] so I combined all these parameters in a log-normal distribution:
model {
skill_effect ~ normal(0, skill_dev);
difficulty_effect ~ normal(0, difficulty_dev);
secs ~ lognormal(mu + skill_effect[uids] + difficulty_effect[dates], sigma);
}
Here, I've defined skills and effects to be normally distributed
around 0, effectively normalizing them.3 [3 Actually… it's
complicated. If I hadn't included the mu parameter, something weird
would have happened, and skill and difficulty would not have been
normalized.] The times are defined to be log-normally distributed, and
the skill and difficulty apply additively to log-seconds.
The secs line can be tricky to read, but that's because of Stan's
vector syntax. If the thing on the left of the twiddle is a vector (or
an array, or whatever), then everything on right that shares an index
space can have its indices left off. It makes for pretty code.
Given this model, Stan can learn the difficulty and skill parameters in a couple of minutes. I used PyStan as the driver:
sm = pystan.StanModel(file="crossbot.stan") fm = sm.sampling(data=munge_data(**data), iter=1000, chains=4)
Note by the way that I know little about statistics, so the 1000 iterations and the 4 chains were chosen pretty randomly. But the \(\^r\) values all came out to 1.0, so I think that means everything is fine.4 [4 Is it?]
This initial version of the model successfully made reasonable choices both for easiest and hardest days5 [5 25 May 2018 was the easiest day and 12 September 2017 was the hardest. I looked them up and they in fact were crosswords I remembered as particularly easy and hard.] and strongest and weakest players.
Adding Saturday effects
One refinement I quickly added was to special-case Saturdays. Saturday mini-crosswords are larger than on other days (7×7 instead of 5×5) and so take longer. To do so, I computed the day of the week for each date, and added it as a new piece of data:
data {
int<lower=1,upper=7> dows[Ss];
}
I then create an array of booleans for whether or not it is Saturday:
transformed data {
int<lower=0,upper=1> is_sat[Ss];
for (j in 1:Ss) is_sat[j] = (dows[j] == 7 ? 1 : 0);
}
Then there's an additional parameter which defines how much harder Saturday is than other days. Actually, at first I created an array of seven effects, one for each day of the weak, in case mini-crosswords get progressively harder throughout the week, but I found that the effects for every day but Saturday were indistinguishable, so I stripped that out.
parameters {
real sat_effect;
}
model {
secs ~ lognormal(... + sat_effect * to_vector(is_sat), sigma);
}
Here, the to_vector call converts the array of booleans into a vector
that can be multiplied by the scalar sat_effect and added to the other
vectors.
Note, by the way, that since we're adding sat_effect to the parameter
of a log-normal distribution, what we're really saying is that
log-seconds increase by sat_effect; in other words, Saturdays have a
multiplicative effect on times. I checked a few users with a lot of
times and the Saturday multiplier seemed pretty close for them, so I
went with this model. Saturdays, it turns out, take roughly twice as
long as other days.
Results
It turns out that it's pretty easy to model large, relatively clean datasets like the crossword times data in Stan, and the results yield a pretty nice ranking of every crossword submitter, by skill:
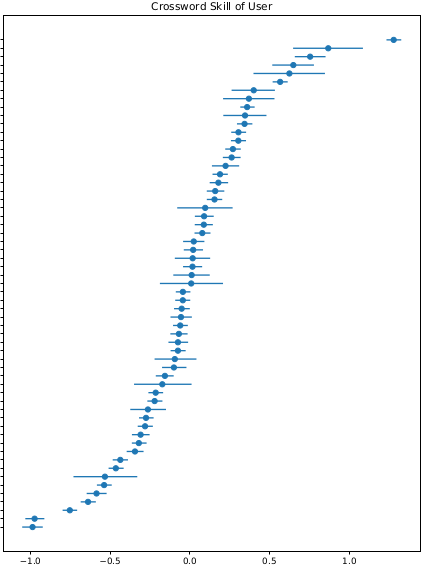
Figure 1: User IDs cropped to protect peoples' pride
I know you can't see the user names there, but it accords quite well with my own estimates of how good various users are. I've also done a bit of validation, where I take a pair of users and compute how many times one has been faster than the other, out of all the times they've done the same crossword. You can compare that number to the difference in their skills, and the results are quite close most of the time.
I'm excited to start using the model to congratulate people on doing well: I've been doing it manually for a few days now, and once a port to Django is complete I'll add it into the Slack bot source code. So far, it really does seem to call out users who do well.
In the future, I also hope to improve the model. In particular, this
model assumes skill is static and unchanging. I want to see how to add
improvement over time.
Footnotes:
It also has matrices and vectors, but I don't know how they differ from arrays of reals.
The fastest time in the dataset is six seconds, and the slowest about nine minutes.
Actually… it's
complicated. If I hadn't included the mu parameter, something weird
would have happened, and skill and difficulty would not have been
normalized.
Is it?
25 May 2018 was the easiest day and 12 September 2017 was the hardest. I looked them up and they in fact were crosswords I remembered as particularly easy and hard.
