You Start Off Bad at Crosswords

The model described in the last post has a single skill term per user. That skill applies to all of the submissions that user makes, which means that if a user gets better over time (or worse), their skill will just represent their average skill over all of their submissions. This means the skill estimate will lag user skill and will consistently over-estimate times.

I wanted to correct for this, and to do so, I needed some model of how people improve over time. So first: what did I mean by time? I decided that the simplest measure of "time doing crosswords" is just how many crosswords you have already submitted. So, I added a variable named nth that, for each user, just counted up from 1 every time they submitted a crossword.¹ [¹ Crosswords come with a submission timestamp, so we use that to handle people who go back and do crosswords they missed out of order.] nth and date are distinct, because people start doing crosswords on different days, sometimes miss days, and sometimes go back and fill in days that they missed.

data {
    int<lower=1,upper=Ds> nth[Ss];
}

Now, I wanted to get a general sense of how nth affects crossword times, without imposing any model. So I added a vector of effects, one for each possible nth value:

parameters {
    vector[Ds] nth_effect;
}

model {
    ...
    secs ~ lognormal(... + nth_effect[nth], sigma);
}

Of course, Stan is going to have a lot of difficulty estimating this nth_effect. For one, non too many people have done a lot of crosswords; only five or six people have done several hundred. Also, nth_effect and difficulty_effect alias, in that submissions on later days mostly also have larger nth values. But still, Stan does produce some estimate, and if you smooth those estimates, you get the following chart (nth on the horizontal, nth_effect on the vertical):

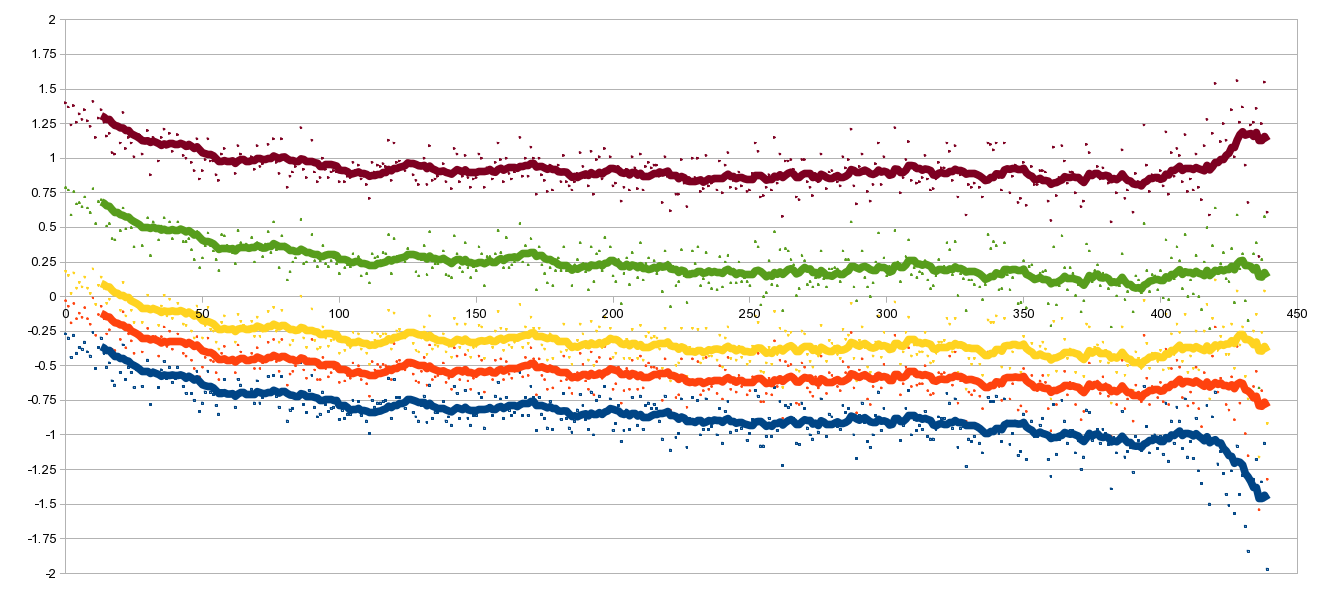
In this figure, focus on the middle (yellow) line. The other lines are 2.5th, 25th, 75th, and 97.5th percentiles. The thick yellow line is the smoothed nth_effect; if you zoom in, you can see little yellow specs, and those are the individual estimates. It is pretty clear that there is some sort of smooth improvement for the first, say, hundred crosswords, and after that point improvement is pretty slow.² [² I don't really know why the yellow line varies around -0.25, instead of around 0; it's probably due to the aliasing.]

The natural interpretation of this data seems to be that there is a significant “beginner's handicap”: people get rapidly better at crosswords, to the tune of exp(.33) - 1 = 40% faster, over the first two or three months of crosswords. After that point, improvement is harder won; it's not even clear that things continue going down after that point.

I decided to add this beginner handicap to the model, so that it could be estimated simultaneously with the other parameters. Estimating simultaneously would mean that beginner handicaps wouldn't taint skill estimates, which would otherwise handicap players until they'd done many crosswords. In Stan:

parameters {
    real beginner_gain;
    real<lower=0> beginner_decay;
}

transformed parameters {
    vector[Ds] nth_effect;
    for (j in 1:Ds) nth_effect[j] = beginner_gain * exp(-j / beginner_decay);
}

Here I am using an exponential decay model for the beginner gain. On day 1, you have a handicap of approximately beginner_gain log-seconds, and that handicap becomes e times smaller every beginner_decay days.

When I estimate this model, I find that beginners are, on average, 68 worse than they'll eventually be, and that handicap decays with a half-life of 49 days. That seems to capture all of the nth effect, however:

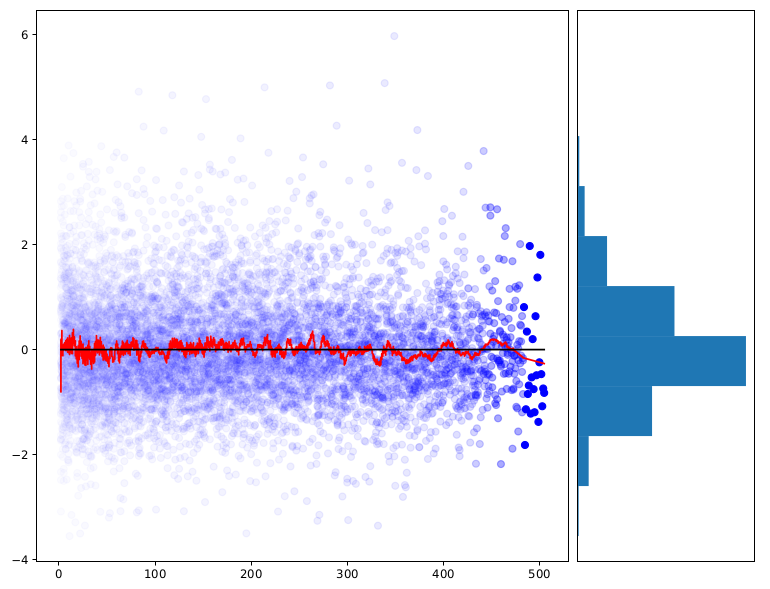
This plot shows the prediction error versus nth when the beginner effect is subtracted out. The red line is a smoothed version of the blue point cloud. As you can see, there's no a clear trend. So this seems to fully capture the effect of improvement over time.

So, overall, you don't get better at crosswords over time, except for a quick shedding of the beginner's handicap over the first few months.

In my next post, I hope to explore a curious incident where Joe did several hundred crosswords over a three days in order to try to get better.

Addendum: I've explored many other modifications to the model, including different learning effects and also bigger modifications like trying to find latent factors behind each crossword's difficulty, and ultimately the model described here seems to be best.