A new era for Herbie

About a year ago, the Herbie team, lead by Brett and Oliver, published Combining Precision Tuning and Rewriting at ARITH'21. While ostensibly that paper was about incorporating precision tuning into Herbie, in reality it was about slightly more than that—it was about teaching Herbie about program cost, and having Herbie find not just the single most accurate variation of your input expression, but about finding a whole cost-accuracy trade-off curve.

This idea of a cost-accuracy trade-off curve is natural in numerical analysis and has become a big focus of my work. After all, if you're not concerned about performance at all, why not use some kind of high-precision software floating-point with thousands of bits? So, since that's absurd,¹ [¹ Of course, this is what analysis tools like Herbie sometimes do—but it's too slow for most numerical programs.] there's clearly some kind of cost-accuracy trade-off that numerical programmers are pursuing.

Moreover, the right cost-accuracy trade-off depends a lot on the application. In my work with Ian on OpTuner, we did a case study with a ray tracer where dozens of bits of error were acceptable, largely because eventually every pixel is stored in 8 bits (per channel) anyway. But that wouldn't be appropriate to most domains. In other words, the developer should decide how to trade off cost for accuracy, not the tool developer.

By contrast, showing the developer a cost-accuracy trade-off curve lets them make their own decision. Importantly, a cost-accuracy trade-off curve is simple to navigate, because it is sorted. The developer can pick some point to start with, and then either choose more accurate or lower-cost points if test results aren't quite as good as desired. And the starting point can be chosen based on the developer's goals—the most accurate point, the lowest-cost one, the lowest-cost point that meets some accuracy threshold, the most accurate implementation no slower than the current one, or anything else. Typically, I've found that cost-accuracy trade-off curves in numerics are small, with maybe a dozen good trade-offs available among thousands of options. That makes all of this pretty accessible.

Note that I've been saying "cost" here, not speed. That's because there's a lot of different types of cost a developer might be concerned with. Speed is one of them, but even speed could mean latency, or it could mean throughput. But cost can also mean memory use² [² A big advantage to lower-precision data types is precisely that they use less data per point, which helps if memory or communication is a bottleneck.] or even just simplicity—most developers are not willing to make their code massively more complicated for minor gains in accuracy.

So today I merged a change that makes Brett and Oliver's cost-aware Herbie the default way to run Herbie. This cost-aware Herbie has been available for a while—it was released in Herbie 1.5—but until now it was ruinously slow, running for minutes to hours on individual examples. Thanks to some recent optimization work, that's been dramatically improved, to the point that cost-aware Herbie is only about twice as slow as accuracy-only Herbie. Since Herbie's also been getting faster in the mean time, this means that the next version of Herbie—1.7³ [³ Or maybe 2.0 to celebrate the magnitude of this change]—will be no slower than Herbie 1.5, the release when we merged cost-aware mode but kept it off by default.

Now, every time you run Herbie you'll get not just a single most-accurate program, but a range of programs with different costs and accuracies. (For now, the cost metric is pretty simplistic, but we plan to make it configurable in the longer term.) There's also a little visualization of those costs and accuracies, which for now looks like this:

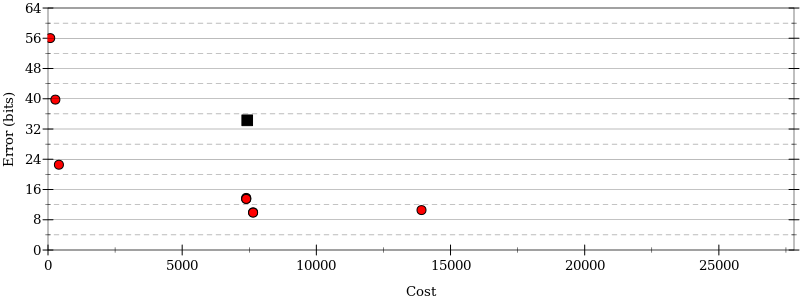
Here the black dot is the initial program input by the user (here, a variant of the quadratic formula) while the red dots are the options proposed by Herbie, which include some very fast programs (which use crude approximations to the quadratic) and some very accurate programs (which use a variety of numerical tricks).

Frankly, I think this is a huge change, and will make Herbie much more useful for lots of people. We commonly get bug reports, for example, asking whether some costly Herbie result is really necessary to achieve low accuracy; now, Herbie will just offer the user both options. Similarly, some users want to use Herbie to improve speed, not accuracy; now, it can do that, and in an accuracy-aware way.

That said, there's more to do to leverage Herbie's new capabilities. Besides trying to make it faster (something we're always trying to do), a change this big also necessitates lots of adjustments elsewhere, from re-tuning Herbie's default parameters to improving Herbie's UI and visualizations to better support multiple outputs. That'll be our focus for the next while. If we're lucky, enough will be done by next summer that we will be proud to call the next release Herbie 2.0.