Optimizing Pruning in Herbie

Pruning is an essential part of Herbie. At a high level, Herbie has three phases: first, it samples a bunch of points it can use to evaluate how accurate a program is; then, it generates a bunch of variants of the program; and then it combines the best variants together in a process called regimes. Pruning happens in the middle phase, where we're generating variants; it keeps the set of variants from growing too large.

We think of pruning as solving a set cover problem. Basically, we have a set of programs and a set of points. Each program has some amount of error on each point. We want to keep the programs with low error and throw away the ones with high error. However, different programs can be better on different points, so really our goal is to prune away as many programs as possible, while maintaining the best program on each point. This would be easy, except that it's pretty common for two programs to be tied at a point. In this case, we don't need to keep both of them, but we do need to keep one of them. This is why it's a kind of set cover problem; you can think of each program as being the set of points it is best at, and we need to cover all points with the fewest possible programs.

Luckily, we don't need to solve this set cover problem exactly—lucky, because set cover is NP-complete. And there's a good approximation algorithm. It works like this:

1. First, keep any programs that are the only best program at that point. They can't be removed.
2. Any of the remaining programs could be removed because at any point they can only be tied for best.
3. Remove the one that is tied at the fewest point.
4. Repeat.

As we remove programs, some of the programs it was tied with might now become the single best program at that point, so now it won't be removed. As we repeat this algorithm, eventually all programs will be best at some point, and at that point the loop terminates. There's a theorem that this will give us at worst twice as many programs as the minimum possible, but honestly that's not too important. Basically, this is the algorithm pruning implements.

Now, pruning is especially important and tricky for Pareto-Herbie. Pareto-Herbie tries to find not just the single most accurate program, but a range of programs with varying speed and accuracy. This means that there's many more programs than in regular Herbie, so pruning takes longer. We don't normally run Pareto-Herbie, because it's too slow, but recently I had CI fail because Pareto-Herbie was timing out, and I decided to look into why. It turns out it was mostly pruning!

Let's pick a representative example. I'll choose the 2tan benchmark, which runs Herbie on the expression

tan(x + eps) - tan(x)

I can run Herbie reproducibly like so:

racket src/herbie.rkt report --seed 1 --profile --num-iters N --pareto 2tan.fpcore out/

Here I've fixed the random seed, turning on profiling, switched to Pareto-Herbie mode, and also set the number of iterations. As we begin our optimization journey, the default four iterations run for effectively forever, so I'll start by setting --num-iters to 2, and as pruning gets faster we'll bump it to a more reasonable figure.

Before we optimize anything, this benchmark takes about 69 seconds to run.

Now, over the years we've built a variety of powerful internal tooling, which can show where this time is spent. First, there is the time bar, which is a kind of timeline showing how Herbie spends its time. It looks like this:

Three colors stand out. There's a bit of yellow in the beginning—that's the sampling step. Then there's a bunch of purple—that's pruning. Finally, there's some red—that's regimes. If you look carefully, there are multiple yellows and reds; those are different subphases. There are also some barely visible other parts of the middle phase in green and orange; we won't be looking at those much.

The basic upshot of all this is that pruning takes up a substantial portion of the runtime. We can get some more detailed information on that by looking at the profile. Now, in Herbie we have this slick web-based viewer for profiling data, which makes it really easy to dig into a gprof-style profile and find the functions we're interested in. For pruning, it looks like this:

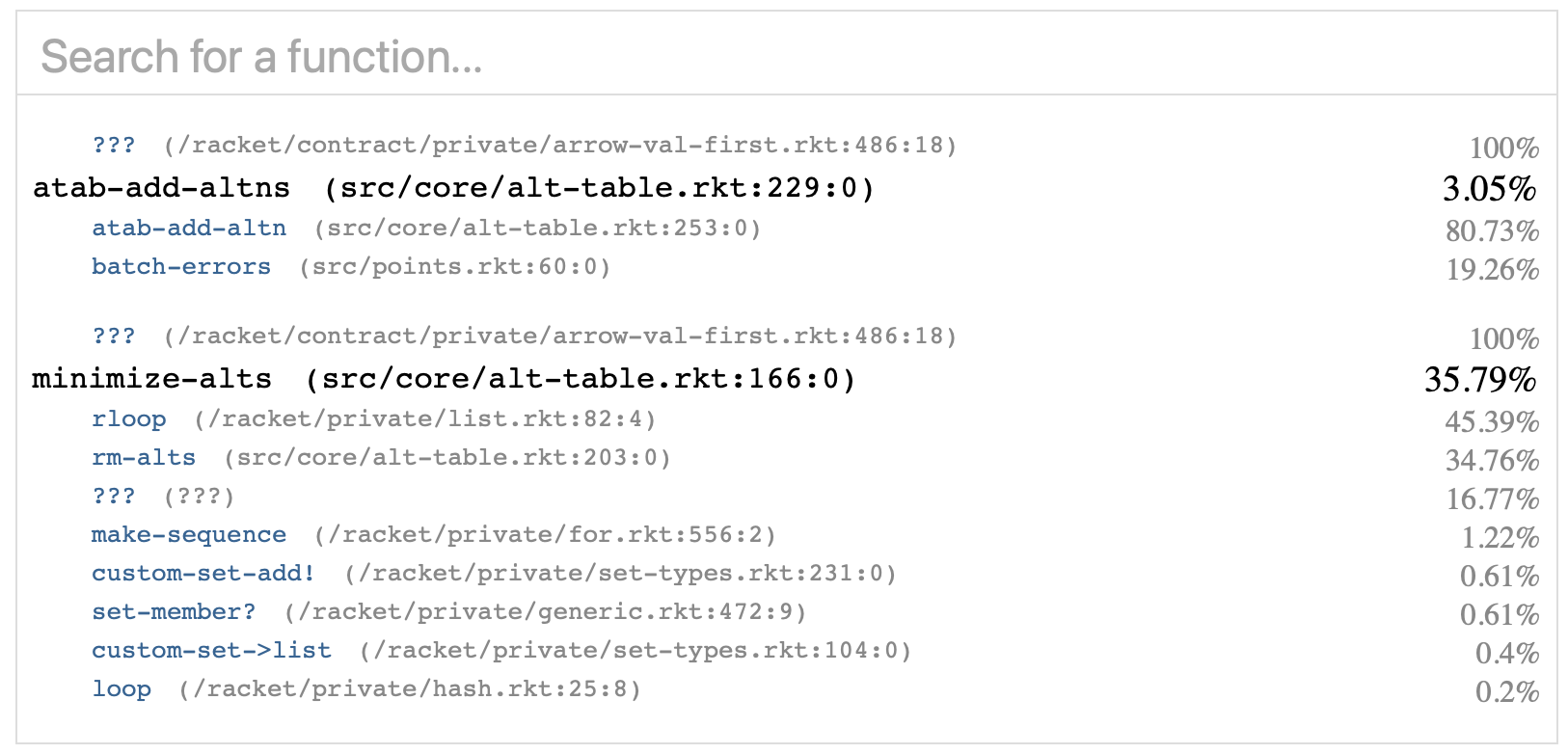
If you haven't read gprof-style profiles before, I've highlighted two functions in the Herbie codebase: atab-add-altns and minimize-alts. On the right beside the function name is its portion of total run time: 3% for atab-add-altns and 36% for minimize-alts. Above the function name are its callers, and below are the functions it calls. The numbers next to those show the percentage relative to the chosen function. For example, minimize-alts spends 45% of its time inside rloop. We'll look there first.

Now, let me give you a quick grounding in the code itself so you can follow along. The actual code is in the git history if you want to read it yourself.

Pruning is organized by a data structure called an "alt table".¹ [¹ "Alt" is Herbie's internal data type for generated programs.] It is a bidirectional index between points and the programs that are best at them. That is, it is:

1. A hash table from programs to a list of points that that program is (tied for) best at.
2. A hash table from points to a hash table from costs to a list of programs (tied for) best at that point and cost.

There are some other tables, but they won't be important to this blog post.

The atab-add-altns function is the entry-point into pruning. It has three steps:

1. Take each program and compute its error on each point, by calling batch-errors.
2. Add each program to the alt-table, updating the two hash tables, by calling atab-add-altn.
3. Minimize the resulting alt-table, using the algorithm described above, by calling minimize-alts.

If you look at the profile above, you'll see that batch-errors, step 1, is about 20% of the time and atab-add-altn, step 2, is about 80% of the time. Weirdly, there's no entry for step 3! That's because atab-add-altns calls minimize-alts in tail position, meaning that when minimize-alts is on the stack, atab-add-altns no longer is. This is one of the many reasons I think tail call optimization is a mistake, but let's not focus on it. The point is that if you add minimize-alts back into the atab-add-altn runtime, you see that in fact atab-add-altn spends about 92% of its runtime in step 3, about 6% in step 2, and about 1% in step 1. So let's focus on step 3, minimize-alts.

The minimize-alts function is pretty complicated, with a variety of internal helper functions. But at a high level, it is a tail-recursive loop which:

1. Finds all the programs that are the only best program at a point, in get-essential
2. Gets the complement, the set of all programs that are potentially removable, in get-tied-alts
3. Picks the worst one in worst
4. Removes it from the alt-table in rm-alts

It then loops. Unfortunately, the same tail call issue makes it difficult to correlate these names to the profile above. I do see rm-alts in second place, at 35% of run time, but what is rloop and ????

Let's start with our top time sink, the mysterious rloop function. This is something defined in the Racket core packages, in racket/private/list. The line number doesn't exactly match, but if you look up the current version of that file, you'll see that rloop is part of do-remove*, which is part of remove*. And if you look up the get-tied-alts function, you see that it is defined as:

(define (get-tied-alts essential-alts alts->pnts)
  (remove* essential-alts (hash-keys alts->pnts)))

Basically, this takes the set of "essential" programs, those that are the single best program at a point, and removes them from the list of all programs to get all the programs that are potentially removable.

How could this take so long? Well, the issue is that even once we're done pruning, it's common to have a few hundred programs, almost all of them essential. So we are removing a list a few hundred long from another list a few hundred long. But remove* operates on lists and does \(O(n^2)\) list set subtraction, so this step takes a long time.

Luckily, the fix is easy. One thing we can do is use Racket's hash sets:

(define (get-tied-alts essential-alts alts->pnts)
  (set->list (set-subtract (list->seteq (hash-keys alts->pnts)) (list->seteq essential-alts))))

This works and brings Herbie's run time from 69 seconds to about 57 seconds, a huge gain! But there's an even better option: why not compute the set of tied programs right away, instead of first computing the essential ones and then taking the complement? It turns out that get-essential starts with an empty set and adds programs to it one by one. We can instead start with the set of all programs and remove them one by one:

(define (get-tied-alts alts->pnts pnts->alts)
  (define tied (list->mutable-seteq (hash-keys alts->pnts)))
  (for* ([cost-hash (hash-values pnts->alts)]
         [rec (hash-values cost-hash)])
    (let ([altns (cost-rec-altns rec)])
      (cond
       [(> (length altns) 1) (void)]
       [(= (length altns) 1) (set-remove! tied (car altns))]
       [else (error "This point has no alts which are best at it!" rec)])))
  (set->list tied))

This is slightly faster (53 seconds) and also a lot cleaner.

Now the profile looks like this:

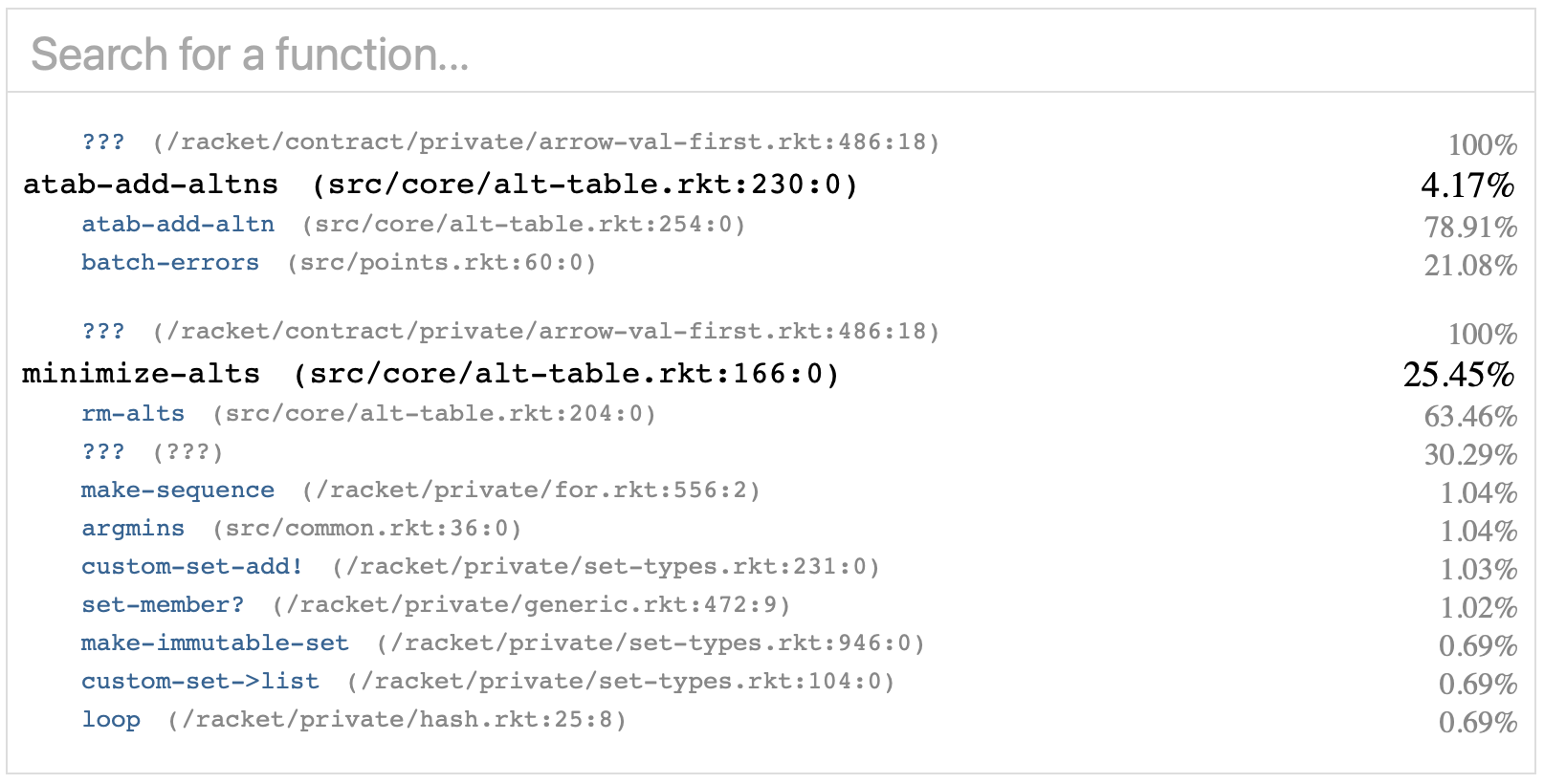
Note that minimize-alts now takes less time, but atab-add-altns now looks like takes more. It didn't actually get slower—it's just that its time equal time is now divided by a smaller total, leading to a larger percentage. So now the next biggest thing to focus on is rm-alts.

The job of rm-alts is to remove a program (or multiple programs, in principle, though it's not called that way) from the alt table. It's called once every pruning iterations. And it spends all of its run time in…

Ah, our old friend remove*. It's called in rm-alts when rm-alts updates the set of programs that are best at a point, to filter out the program we're removing.

Again we need to replace it with set-subtract. This brings the total run time down from 53 seconds to… 55 seconds? It looks like this didn't help at all, probably because there's a lot of conversion here between lists and sets.

But actually—since we're only removing a single program, do we even need a set at all? We just need to filter a list to remove a specific element. Let's make a specialized version of rm-alts that removes only a single program, and call that. (I'll keep the more general version, even through we're not calling it anywhere right now, because later we'll need it.) Since we're removing just one program, we can use remq instead of remove*, which should be much faster. And indeed it is—it takes runtime down from 53 seconds to 49 seconds.

Even after this, however, our specialzed atab-remove-alt is the biggest portion of minimize-alts. And, unhelpfully, its profile looks like this:

That ??? entry is annoying, but in this case it refers to hash operations (which are probably provided from C code and therefore don't appear in the stack). This isn't a bit surprise, because atab-remove-alt, like most of pruning, uses immutable hash tables. That leads to a lot of copying, mostly totally unnecessary.

Since all of this is being done internally to a single function, minimize-alts, we should be working mutably instead. That would reduce copying. In fact, ideally we'd be using mutable sets that we could call set-remove! on. We also, ideally, wouldn't be updating any other part of the alt-table, since we only really care about the set of programs that cover each point.

This suggests a new structure to minimize-alts:

1. First, convert the alt-table to a bunch of mutable sets.
2. Prune on those mutable sets, producing a list of programs to remove.
3. Construct a new alt-table with those programs removed.

I'll call the bunch of mutable sets a set-cover data structure:

(struct set-cover (removable coverage))

Here removable will be the set of removable sets, and coverage will be which sets cover each point. We can build both during get-tied-alts, which I'll rename atab->set-cover:

(define (atab->set-cover atab)
  (match-define (alt-table pnts->alts alts->pnts alt->done? alt->cost _ _) atab)

  (define tied (list->mutable-seteq (hash-keys alts->pnts)))
  (define coverage '())
  (for* ([cost-hash (hash-values pnts->alts)] [rec (hash-values cost-hash)])
    (match (cost-rec-altns rec)
      [(list)
       (error "This point has no alts which are best at it!" rec)]
      [(list altn)
       (set-remove! tied altn)]
      [altns
       (set! coverage (cons (list->mutable-seteq altns) coverage))]))
  (set-cover tied coverage))

We can now remove a set from a set-cover without doing any hash operations at all:

(define (set-cover-remove! sc altn)
  (match-define (set-cover removable coverage) sc)
  (set-remove! removable altn)
  (for ([s (in-list coverage)])
    (set-remove! s altn)
    (when (= (set-count s) 1)
      (set-remove! removable (set-first s)))))

Note that as I remove a program from the set-cover, I also remove singletons from the set of removable sets.

Now minimize-alts will construct the set-cover, remove programs from it one by one until there aren't any more to remove, and finally construct a new alt-table using the old rm-alts:

(define (minimize-alts atab)
  (define sc (atab->set-cover atab))
  (let loop ([removed '()])
    (if (set-empty? (set-cover-removable sc))
        (apply rm-alts atab removed)
        (begin
          (define worst-alt (worst atab (set->list (set-cover-removable sc))))
          (set-cover-remove! sc worst-alt)
          (loop (cons worst-alt removed))))))

This is a big rewrite, but the fact that it introduces a new, simpler datastructure is a good thing. And it's fast:

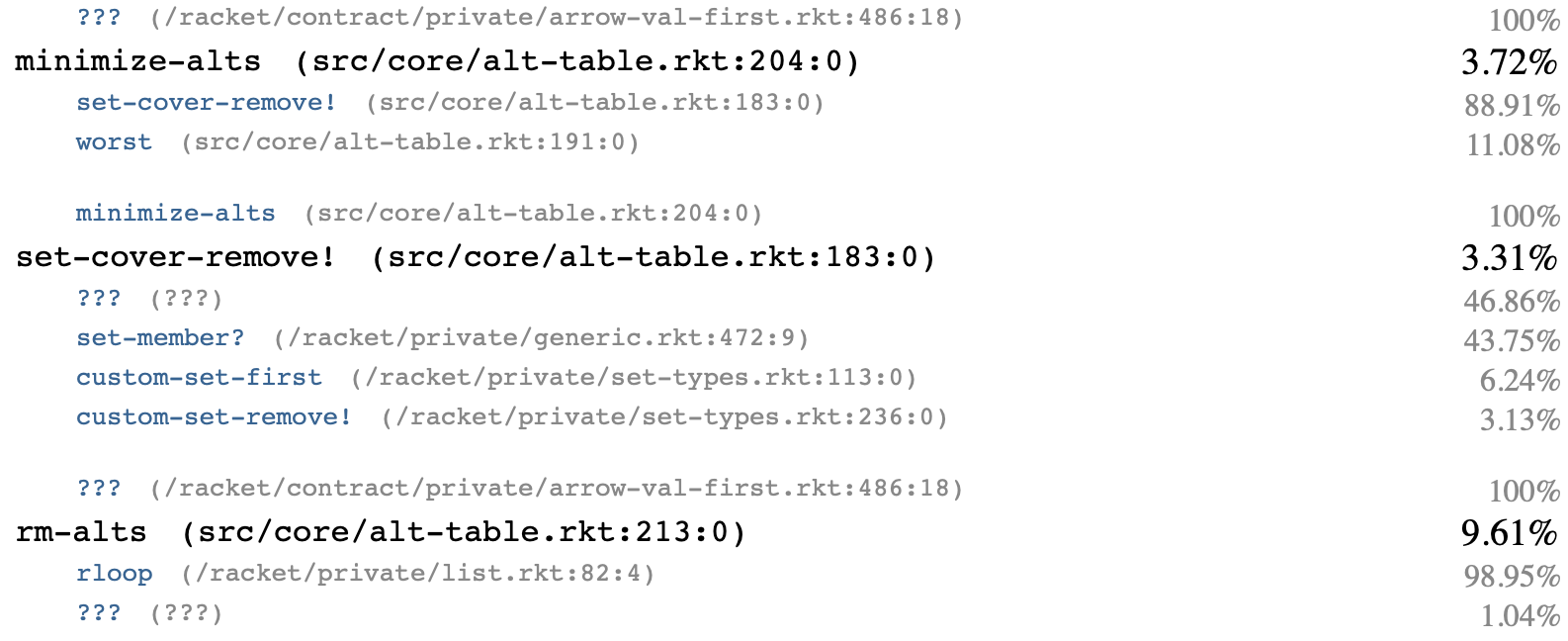
Almost all the time now is in rm-alts, which now runs only once, at the end of minimize-alts. And now that we're removing lots of programs at once, it does make sense to change its use of remove* to a set-subtract, which leads to a further speed-up, taking us from 49 seconds to about 48 seconds.

With all of these optimizations, the profile now looks like this:

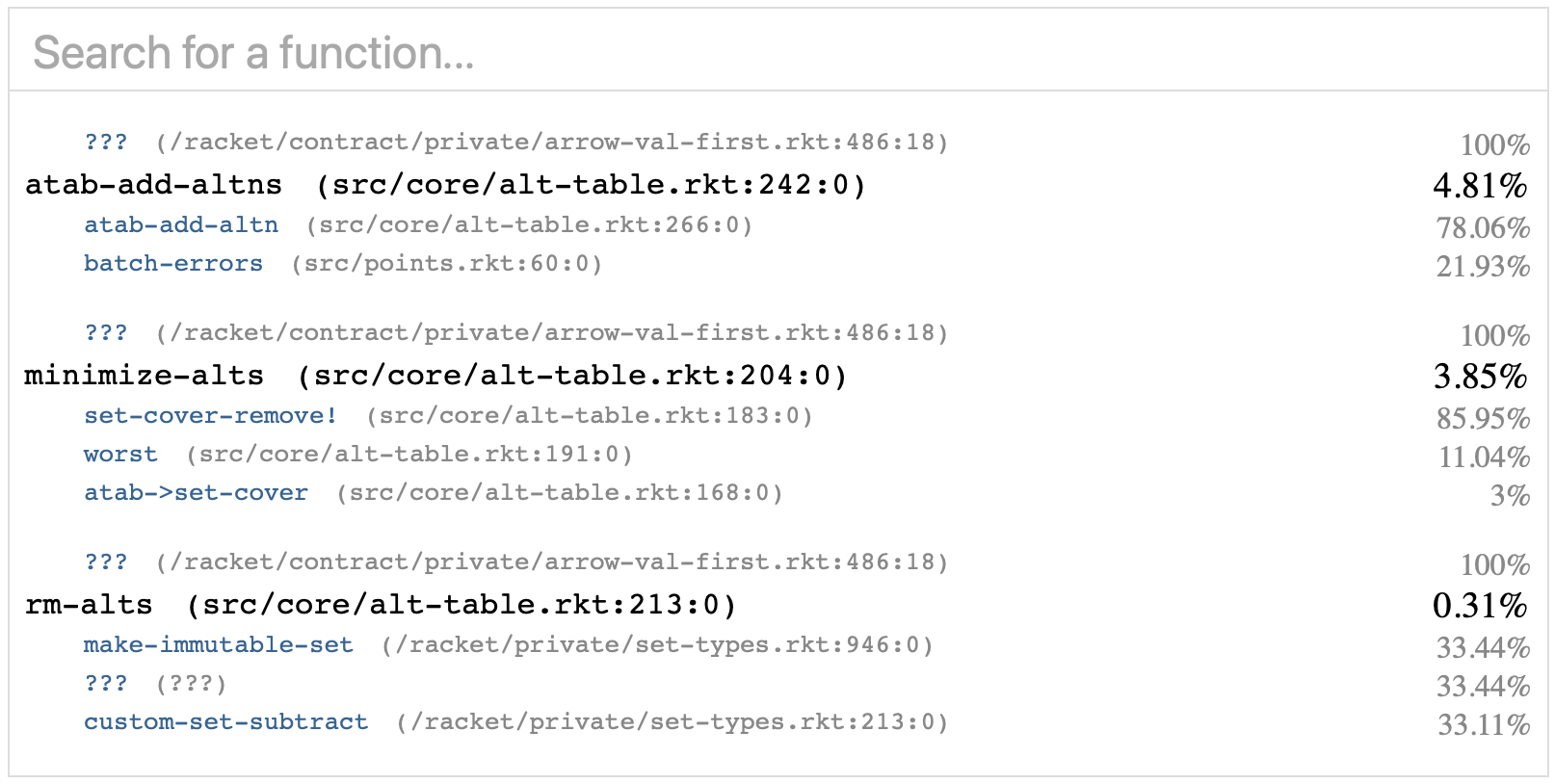
Overall, about 10% of run time is spent inside pruning, down from about 40%. It's about time to make the problem harder by raising the number of iterations from 2 to 4. This will increase the amount of pruning by a lot, without much affecting the amount of regimes (since it only runs once), so it will mean a much larger percentage of run time is spent in pruning. That will make further optimization more valuable and more visible.

Going all the way to 4 iterations takes overall run time to 184, with… 18% spent in pruning? Wait, what?

Ah—at this point I found a bug. You see, the input to regimes is the set of all programs that ever made it past pruning. That list is updated by atab-add-altn. But atab-add-altn runs before pruning, meaning that even programs that are pruned away were still making it to regimes, which runs slower with more inputs. Luckily, this was an easy fix—I just needed to update the list in atab-add-altns after minimize-alts. Fixing that bug takes us from 184 seconds to 96, and pruning from 18% to 26% of run time.

Conveniently, this bug also means that minimize-alts is no longer a tail call, which makes the profiles easier to read. Let's actually just take this chance to rename and reorganize the code a bit, leading to the following profile:

Interestingly, we're now seeing the positive effects of the minimize-alts optimizations: it is now only 50% of total pruning run time, with atab-add-altn taking up almost 40%.

If we dig into minimize-alts we see that most of the run time is in set-cover-remove!, as we expected, and that spends about half its time in ??? and about half in set operations. That makes sense, because set-cover-remove! is basically a tight loop with three set operations inside. But can we skip some of that work?

One easy insight is that if a point is ever covered by a single program, then (because that program can never be removed) it will never be updated. So we can skip those sets and never update them. One easy way to do that is to allow coverage to store either a set, or the #f value, where #f means to skip an entry. (We could filter out #f values, but that would require copying the whole list, which sounds slow to me…) That's easy to code up, and just requires a few changes: change coverage to be a vector instead of a list (so it can be modified), test each entry of the loop, and set entries to #f when they're down to one element:

(define (set-cover-remove! sc altn)
  (match-define (set-cover removable coverage) sc)
  (set-remove! removable altn)
  (for ([i (in-naturals)] [s (in-vector coverage)] #:when s)
    (set-remove! s altn)
    (when (= (set-count s) 1)
      (set-remove! removable (set-first s))
      (vector-set! coverage i #f))))

But, oof, no, this doesn't help at all, taking run time from 96 seconds back to 150 seconds. Now, it's not entirely clear to me why—performance for a high-level language like Racket is often pretty opaque, so sometimes a seemingly-effective change just doesn't work for some reason. Anyway, let's file this idea away for later but backtrack for now.

A surprisingly-large percentage is spent in set-member? (it isn't called directly but is called by set-remove! to check if the element being removed is in the set) and by wrapper functions like custom-set-remove! that we can probably optimize.

This overhead is probably because sets are a generic datastructure in Racket, meaning that we need to do some kind of lookup in the generics machinery. I did ask Sam in the Racket Slack whether it's possible to avoid this overhead, but he seemed to think writing our own set would be easier. So why not?

Now, in Racket, sets are implemented via hash tables, and that's a good design for sets in general, but in our case that seems less than ideal, since it means that our hot path will have a lot of hashing. Could we do better with flat vectors?

Here's my plan: each entry of coverage will be a vector of programs, or #f entries for programs that we've removed. To remove an entry, we scan the whole vector looking for it—the theory here is that the vectors are short so the scan is better than hashing. As we scan, we can also store a count and an element, so we'll only need to do a single pass through this vector. It looks like this:

(define (set-cover-remove! sc altn)
  (match-define (set-cover removable coverage) sc)
  (set-remove! removable altn)
  (for ([s (in-list coverage)])
    (define count 0)
    (define last #f)
    (for ([i (in-naturals)] [a (in-vector s)])
      (cond
       [(eq? a altn)
        (vector-set! s i #f)]
       [a
        (set! count (add1 count))
        (set! last a)]))
    (when (= count 1)
      (set-remove! removable last))))

The code is getting uglier and uglier—there's now some local mutation, ugh—but that's a cost we'll have to pay if the speed-ups are good. And they are: run time is now down to 85 seconds, with a profile that no longer emphasizes minimize-alts:

So it's time for us to turn our attention to atab-add-altn.

The atab-add-altn function is pretty complicated, with several steps. First, we do some simple tests to avoid adding an program to the alt-table if it's going to be pruned away later. Then, if we pass that test, we add the program to the alt-table in four steps:

1. Figure out which points the program is best at, or tied for best at, in best-and-tied-at-points.
2. Any points it's best at, other programs are no longer best at, so remove those points from their maps in remove-chnged-pnts.
3. Replace the existing list of best programs on those best points in override-at-pnts.
4. Add it to the existing list of best programs on the tied points in append-at-pnts.

If we glance at the profile, it's clear which one is slowest:

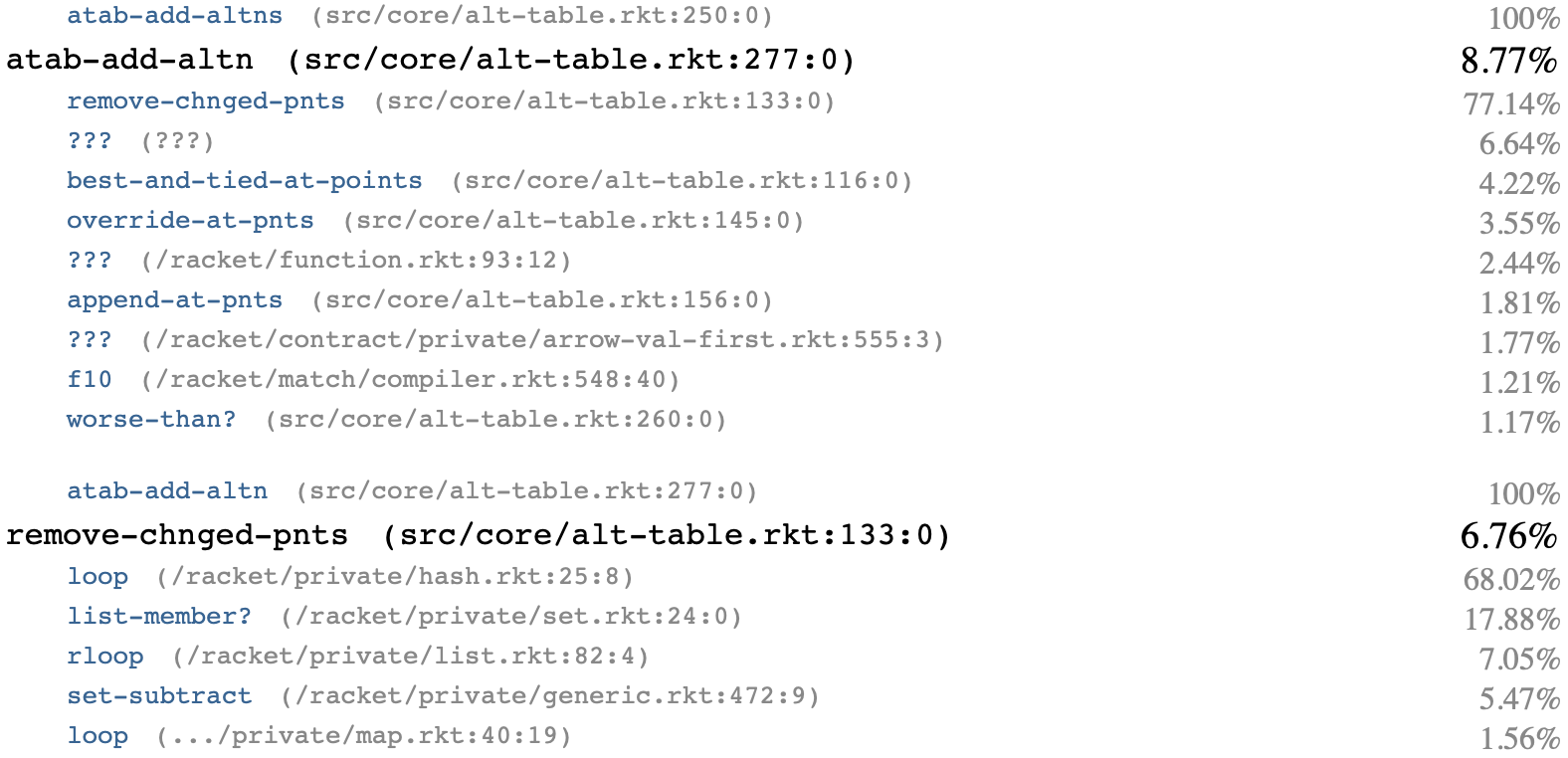
So we need to look at remove-chnged-pnts. But weirdly, the slow part is two functions that implement Racket's hash-keys and set-member? functions. And that's probably due to this dumb bit of code in remove-chnged-pnts:

(for* ([entry chnged-entries] #:when (set-member? (hash-keys entry) cost)

Clearly this is checking whether cost is a key of entry, but it's doing it the slow way, building a list of all the keys and the scanning through that list. There's a clearer and faster hash-has-key? function. Just making that small change gets us to this profile:

By the way, I also noticed that remove-chnged-pnts spent time in rloop, which I already recognize as being part of remove*, so I found and fixed that line as well:

(set->list (set-subtract (list->seteq (hash-ref alt->points altn)) chnged-set))

This leads to another solid speedup

So we're now looking at the following profile:

The profile is starting to flatten out, with more and more things contributing to run time; the only large contributor is set-cover-remove!, and that's already been optimized pretty heavily. Moreover, the total time spent in pruning is down from about 40% to about 8%, with almost all time now spent in Herbie's regimes pass. These facts suggest that we've picked all of the low-hanging fruit in pruning, signaling the end of this optimization pass and therefore this blog post.