Zippers, Part 2: Zippers as Derivatives
A zipper is a purely functional cursor into a data structure. The cursor can be moved around the data structure, and parts of the data structure close to the cursor can be updated quickly. This second of four parts discusses the theory of algebraic data types, and how the operation of creating the zipper of a data type may be mechanized.1 [1 This transformation was first discovered by C. McBride. A later paper of his, elaborating on the concept, is available as (PDF). When I wrote this blog post, years ago, the name C. McBride meant nothing to me. Now, as a graduate student in programming languages with an interest in dependent type theory, I'm astounded to realize that my first McBride paper was this one.]
Algebraic Data Types
An algebraic data type is one way of combining types into bigger types. For example, a 3-dimensional coordinate is made up of three coordinates, and we can treat a binary tree of strings as a certain structure built out of strings, which is a certain structure built out of characters.
def/adt StringBinaryTree <-
Node String StringBinaryTree StringBinaryTree
Empty
def/adt String <-
String Char String
End
Above, I defined two algebraic data types:
- A
StringBinaryTreeis eitherEmtpyor aNodecontaining oneStringand twoStringBinaryTreeelements. - A
Stringis either anEndor aStringwith aCharand aString(presumably, a first character and the rest of the string).
Thus an algebraic data type permits two operations on types. Given
two types A and B, we can consider the types (Product A B) and
(Left A) (Right B): the type which contains both A and B, and
the type that contains either A or B. Mathematically, we can
write these two combinations of types α and β as α × β and α + β: the
product type (type α and type β) and the sum type (type α or type β).
Algebra on Data Types
Why do we use the sum and product notations? Because these operations on types behave a lot like addition and multiplication of other things, such as numbers.2 [2 In fact, algebraic data types form a semiring.]
To see how, let's prove all of the standard axioms for numbers. For
example, we can easily prove that both sum and product types are
commutative. Why? Because we can easily rewrite code that uses adt
(Product A B) to use adt (Product B A); similarly, we can easily
rewrite code that uses adt (Left A) (Right B) to use adt (Left B)
(Right A), just by switching the order of A and B. Thus, the two
data types are the same in the sense that they carry the same
information. So in that way, we might say that α × β = β × α and α +
β = β + α.
Another axiom satisfied by numbers is the associative law. Again, this is clear, because it just requires us to be able to modify our source code to not care how data types are nested.
But what about identities? For example, is there a data type we can
product with something to get the same thing? At first, it might seem
impossible. But consider: if one of the two elements of our product
(of our pair) carries no information, we can just rewrite our code to
ignore it. And what type carries no information? What about the type
of which there is only one instance? If a type has only one possible
value, then that value carries no information (we already know what it
must be). Let's call this type 1 (in some languages like Haskell,
it's written ()). Then the type of 1 × α carries no information
than α itself, and we can easily rewrite code to ignore the useless
pair.
Similarly, we need an identity for addition. The unit type 1 is not
the identity, since the type 1 + 1 does carry some information: we
know whether the left or right unit value is chosen3 [3 In fact, this gives us exactly one bit of information, just like a boolean. Booleans can be defined as adt True False, that is, as the sum of two unit types.]. Instead, we
need an alternative that we know will never be taken. To do that, we
invent another type, the zero type (in some languages like Haskell,
it's written ⊥). It has no values at all; thus, we know that its
alternative in a sum type can never be taken. Similarly, \(1 \times 0\) must
be \(0\), because there is no way to instantiate the second element of
that pair, and thus there are no values of this type.
The final axiom we want to show is that multiplication distributes over addition. Again, this is easy to verify.
Algebra on Data Types
Suppose we want to make a data type that might hold any number of some specific type. For example, we want a data type that holds any number of integers. Well, if we call the inside type α, we could say that we want the type \(1 + \alpha + \alpha^2 + \alpha^3 + \dots\). It may not be obvious how to achieve this. But a bit of algebra can explain. If we write \(F(\alpha) = 1 + \alpha + \alpha^2 + \alpha^3 + \dots\), we can manipulate that expression algebraically to obtain \(F(\alpha) = 1 + \alpha F(\alpha)\) (check this for yourself). But this, we see, is the same as the standard definition of a list: a list is either a terminal value (1), or a pair of list item and remainder list (\(\alpha F(\alpha)\)). And, in fact, this is correct, since a list is a data type that holds any number of some other type.
Zippers
Recall that one of the ways we think about zippers is that it is the original data structure, but with a "hole". Reasoning along these lines, what would be a zipper on a pair? That is, what type represents the zipper of \(\alpha^2\)? Well, the pair-with-a-hole is either just the second element of the pair (the first is the hole) or just the first element. So it has data type \(\alpha + \alpha\), or \(2 \alpha\). There's another common operation that takes \(\alpha^2\) to \(2 \alpha\): differentiation.
We demonstrated above that the list type can be represented by \(L(\alpha) = 1 + \alpha L(\alpha)\). Furthermore, as discussed in the previous part, the zipper of a list is just two lists. Let's ruminate on that. If \(L(\alpha) = 1 + \alpha L(\alpha)\), then we can preform some basic algebra to derive \(L(\alpha) = \frac{1}{1 - \alpha}\). But if a list with a (Huet) zipper is just two lists, it stands to reason that a zipper list (let's write it \(L^Z\) for now) should be \(L^Z(\alpha) = (\frac{1}{1 - \alpha})^2\). Again, \(L^Z(\alpha)\) is the derivative of \(L(\alpha)\).
In fact, this is true in general: if we want to add a zipper to a structure, we can just use that structure's derivative. To prove this, we have to prove the basic derivative rules. We'll need to prove that the operation of a zipper works like differentiation on sums and on products (and also has a chain rule). We'll write the Huet zipper operation on some structure α as ∂ α.
So let's start with sums. If we want to add a hole to a sum type, well, then the hole must be in whatever alternative we take. So ∂ (α + β) = ∂ α + ∂ β.

Figure 1: A hole in alternatives is in whatever alternative we choose
What about products? Well, we have a pair of things, and there is a hole in it. Where's the hole? We have two choices: the hole is either on the left or the right. So either the hole is on the left, for a result of (∂ α) β, or the hole is on the right, for a result of α (∂ β). Adding the two gives us ∂ (α β) = (∂ α) β + α (∂ β).
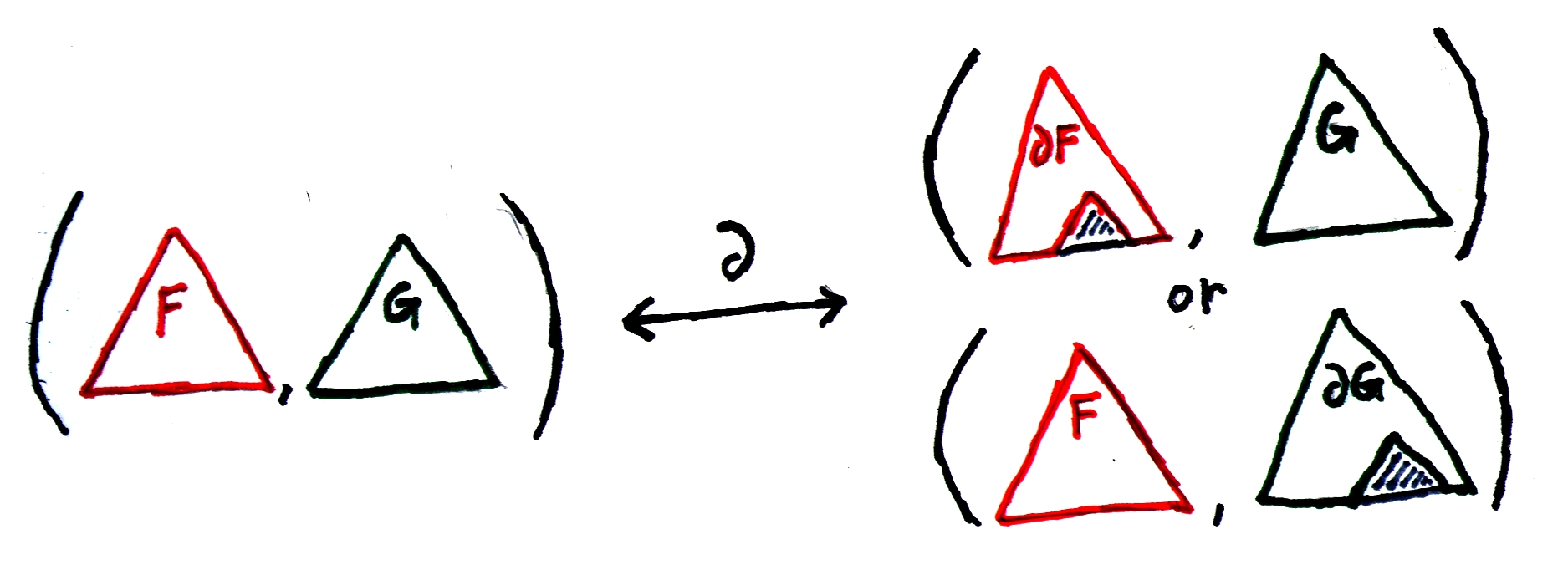
Figure 2: The hole in a pair is on the left or the right
Finally, let's deal with composition: what if we have one structure, α, parameterized4 [4 By parameterized, I mean that one type is built atop another. For example, we write a list of α as L(α), and we say that the list is parameterized over the structure α.] over another type, β? Well, we know that there's a hole inside one of the elements of type β. But how do we represent that? Well, we can break that element out of the larger α structure, leaving behind an type "α with a hole", and then keep that element around as well (with its hole in it). The picture might help.
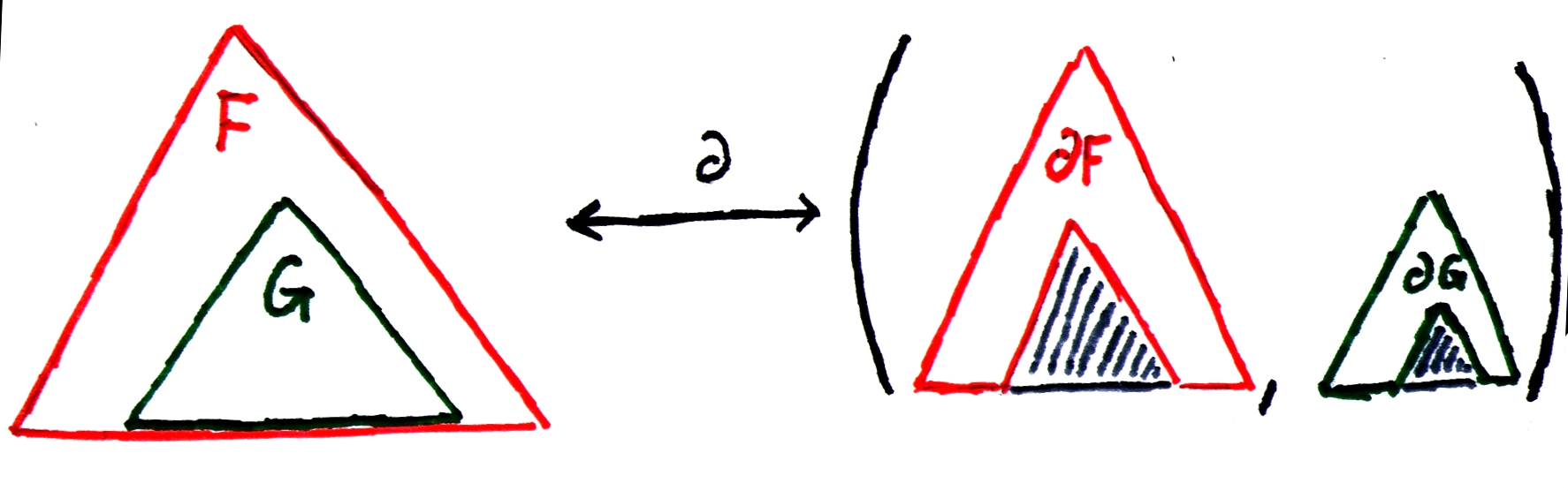
Figure 3: A hole in nested structures
Anyway, in this case, we have an α(β) with a β-sized hole in it (so, (∂β α)(β), where ∂β is "derivative with respect to β") and also a β with a hole in it (that'd be a ∂ β), for an overall type of (∂β α)(β) × (∂ β). This is again exactly like for derivatives of the usual calculus variety, which is what we wanted to prove.
Why we Care
While this is rather pretty (well, maybe only in my opinion…), what are the benefits of this for, you know, programming? Well, one thing we can do is, now that we have a strict mathematical way of getting the zipper of some structure, we can have the computer derive zippers for structures for us5 [5 A language like Haskell isn't quite powerful enough to do this. There's an extension to Haskell called "Generic Haskell", and there is a paper, Generic Haskell: practice and theory (Hinze and Jeuring; PDF) that, among other things, implements zippers.].
But beyond simple animation, let's try to figure out why this is the case. The core concept is that we can imagine our data structure as changing with time. Our zipper represents the difference between the current structure and the future structure — that is, all those nodes that whose pointers we reversed that we'll end up inserting back.
In fact, this way of thinking about the zipper — as a representation of a "paused" computation — is exactly what Kiselyov's zipper is. But that's for part 3…
Footnotes:
This transformation was first discovered by C. McBride. A later paper of his, elaborating on the concept, is available as (PDF). When I wrote this blog post, years ago, the name C. McBride meant nothing to me. Now, as a graduate student in programming languages with an interest in dependent type theory, I'm astounded to realize that my first McBride paper was this one.
In fact, algebraic data types form a semiring.
In fact, this gives us exactly one bit of information, just like a boolean. Booleans can be defined as adt True False, that is, as the sum of two unit types.
By parameterized, I mean that one type is built atop another. For example, we write a list of α as L(α), and we say that the list is parameterized over the structure α.
