Treaps: The Magical Awesome BBT
Treaps are the awesome balanced binary tree. A little randomness makes a tree that is expected to have logarithmic height but is easy to code, requiring none of the special-cases that characterize red-black trees. Here, I code up a complete treap implementation in Lisp (particularly, pylisp).
Table of Contents
Our Goals
Our goal is to create a treap-based implementation of a map. I'll be using Lisp, in particular pylisp; feel free to follow along in any other language.
A treap map supports the following interface:
(get key treap)- Get the value associated with
keyfrom our treap. (in key treap)- Return
#tifkeyis in your treap, and#fif not. (set key val treap)- Return a new treap, which is the same as
the old one except associates
keywithval. (del key treap)- Return a new treap, which is the same as the
old except does not associate anything with
key.
Note that our treap is functional, so set and del return new treaps
with the necessary modifications made. Furthermore, each of these
methods run in \(O(\log n)\) time.
Binary Trees and Heaps
Note
What I'm calling a "binary tree" here is normally called a binary search tree.
Quick review: what's a binary tree? Simply put, it's a tree where each node has both a key and a value, and for each node, the left subtree has smaller keys and the right subtree has larger keys.1 [1 I'm ignoring duplicate keys, but they don't change much.] This rule makes lookups for any key fast: we binary search the keys. But this speed requires the left and right subtrees to be approximately equal in size. When that's roughly true for every node, the tree is called “balanced”.
Balancing
There exist many, many algorithms to “balance” binary trees, ensuring that any node's subtrees are similarly sized, but most of them are horrible, confusing things with thousands of special cases. Which is a pity! Binary trees work well in functional code (unlike hash tables) because they can share structure. And they provide an ordered map, so you can iterate over the keys in order without having to sort.
For example, say you're writing an address book, so you need a map from contacts to phone numbers. With a hash table, you need to sort the contacts to display them in order. By storing the contacts as a binary tree, you transform \(O(n \log n)\) sort into an \(O(n)\) iteration.
So let us embark on a journey to balanced binary trees with treaps.
Heaps
The second data structure treaps build upon is the heap. In a heap, every node has a priority, and this priority is the lowest priority of its subtree. Heaps are often used to implement priority queues, and are otherwise a pretty niche data structure.
Note
Technically, I've described a "min-heap", where the root is the minimum element. In a "max-heap", the root is the maximum element. Normally, one does not actually care which a heap is, since the main property is that the root is extremal.
Tree Rotations
One binary tree can be transformed into another with rotations, which modify the tree while preserving its order properties:
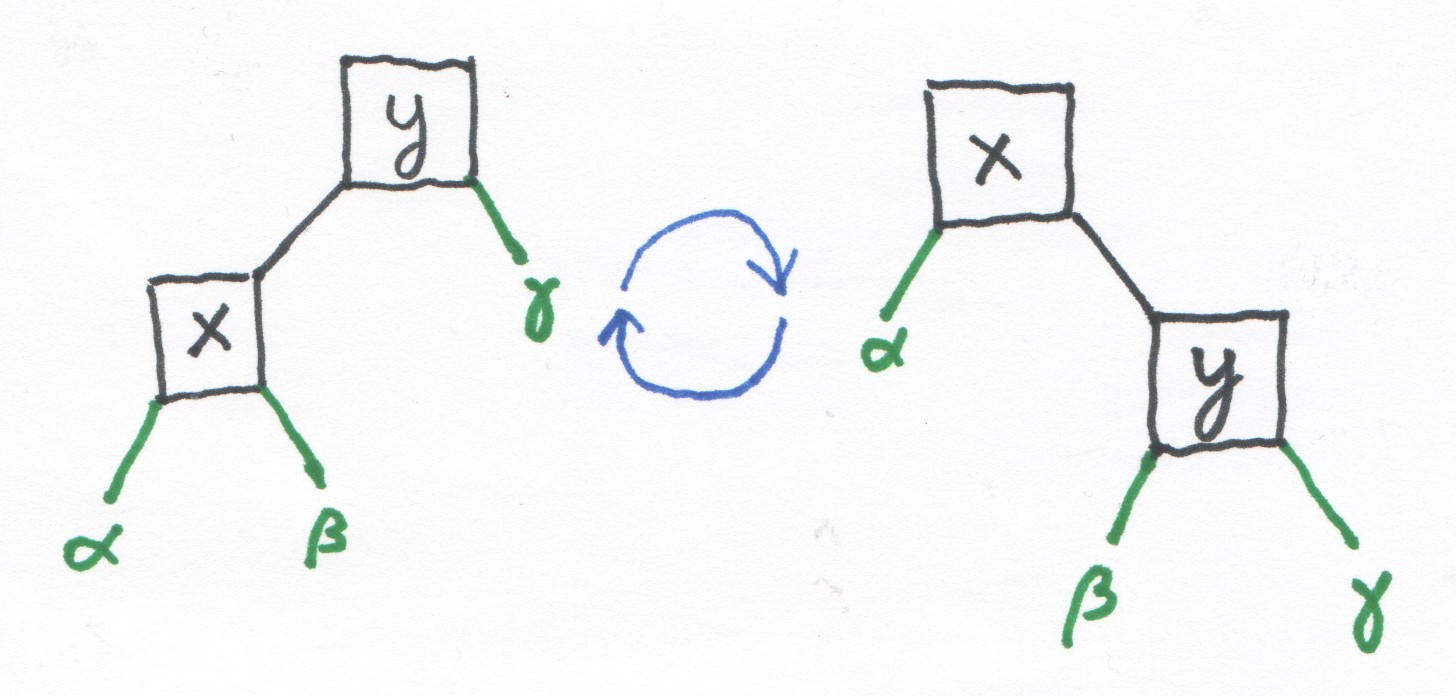
Figure 1: In this diagram, right rotations go left to right, and left rotations go right to left.
In this picture, the Greek letters represent subtrees that don't
change during a rotation. Rotation retains the tree's order
properties: both trees are sorted \(\alpha < x < \beta < y < \gamma\).
This order-preservation is the most important property of the
rotation, but it also moves nodes up and down in the tree—here, x
moves up and y moves down. Another rotation could move x yet further
and further, until it became the root of the tree.
The Basic Idea
A treap is a cross between a binary tree and a heap: each node has both a key and a priority, and the tree is both a binary tree (on the key) and a heap (on the priority).
Now does there always exist a treap for a given set of keys and priorities? Is that treap unique?
A simple argument answers both in the positive. Clearly, the root node must be the node with lowest priority. This partitions the remaining nodes into two sets: those with key less than the root, and those with key greater. Recurse onto each of those sets, building treaps out of them, until there are no more nodes left, and you have a valid treap.
Now, in a map, keys are assigned by the user, but where do priorities come from? A treap assigns the priorities at random; this tends to move values with middling keys into the root of the tree.
Let's prove that this results in a tree with logarithmic height. Now consider the root node, and ask: what's the size of the larger of its subtrees, as a percentage of the total tree? Well, we know that the root of the treap is the node with the smallest priority, and since priorities are chosen randomly, it has a 50% chance of being between the first and third quartiles of keys. Imagine, now, taking some path from the root down. On average, every time we go down two nodes, at least one quarter of the tree is no longer in our subtree. So if there are \(n\) nodes, we expect our path to end after \(2 \log_{3/4} n = O(\log n)\) steps.
Now that the theory is clear, let's implement treaps.
Lookup and Containment
It's time to start programming: spewing out s-expressions at machine gun speeds. Buckle up. First things first, let's define a data structure for nodes:
(class::simple Node (p key val left right))
Unfamiliar with pylisp? This defines a class with fields p, key, val,
left, and right, and also a constructor for this class.
Now, let's implement some methods. First up: the get function. Since
our treap is already a binary tree, we use the standard binary tree
lookup algorithm, completely ignoring priorities:
(def get (key root) (cond ((not root) (signal '(error not-found key get) key)) ((< key root.key) (get key root.left)) ((> key root.key) (get key root.right)) ((= key root.key) root.val)))
Containment, in, is basically identical:
(def in (key root)
(cond
((not root)
#f)
((< key root.key)
(in key root.left))
((> key root.key)
(in key root.right))
((= key root.key)
#t)))
Insertion
Now on to the more difficult modification operations.
How do we insert an element or update a value? Well, we can spider
down to the place where the new node should live using the same
algorithm as get above. But we can't just add the new node there if
its (randomly chosen) priority is larger than its parent's. Instead,
we have to move it upwards in the tree, while maintaining the ordering
property of binary trees.
Well, I've already mentioned that tree rotation move nodes up and down and preserve ordering. So let's implement left and right rotations:
(def left-rotate (node)
(Node node.left.p node.left.key node.left.val
node.left.left
(Node node.p node.key node.val node.left.right node.right)))
(def right-rotate (node)
(Node node.right.p node.right.key node.right.val
(Node node.p node.key node.val node.left node.right.left)
node.right.right))
With that out of the way, let's start on insertion itself.
First, we'll need to import the random module to get priorities:
(use random)
The new node needs a random priority before we inserted, and I'm going to pass that priority up and down the call stack instead of generating it once we get to the leaves of the tree. Trust me on this one.
With that set, here's a rough skeleton for set:
(def set (key val root #:(p (random.randint 0 1000000000))) (cond ((not root) ?) ; Just generate the new node ((< key root.key) ?) ; Recurse leftwards, then do a left-rotation if necessary ((> key root.key) ?) ; Same as the (<) case, but recurse and rotate to the right ((= key root.key) ?))) ; Update existing node. So, just create the new node
Alright, let's fill this baby in. The first case, with an empty treap,
is easy:2 [2 Note that #0, the null object, is my representation of
the null treap.]
((not root) (Node p key val #0 #0))
Next, let's do the last case, where we are updating a value, not adding a new key:
((= key root.key) (Node root.p root.key val root.left root.right))
Note that I'm not updating the priority; it would have been fine to do so, but would only have lead to extra tree rotations later.
We have only the two middle cases left, and they're basically identical. First, we recurse to insert into one of the subtrees. But that might have upset the heap property, so we may have to carry out the appropriate rotation:
((< key root.key) (let (new (Node root.p root.key root.val (set key val root.left #:(p p)) root.right)) (if (< new.left.p new.p) (left-rotate new) new))) ((> key root.key) (let (new (Node root.p root.key root.val root.left (set key val root.right #:(p p)))) (if (< new.right.p new.p) (right-rotate new) new)))
Putting it together, we have:
(def set (key val root #:(p (random.randint 0 1000000000))) (cond ((not root) (Node p key val #0 #0)) ((< key root.key) (let (new (Node root.p root.key root.val (set key val root.left #:(p p)) root.right)) (if (< new.left.p new.p) (left-rotate new) new))) ((> key root.key) (let (new (Node root.p root.key root.val root.left (set key val root.right #:(p p)))) (if (< new.right.p new.p) (right-rotate new) new))) ((= key root.key) (Node root.p root.key val root.left root.right))))
Yeah, it looks big now, but all the pieces make sense. And note that
this is functional—not a single set! call. Recursion mixes oh so
well with functional programming. Yes it does.
Split & Merge
Before we tackle deletion, let's take a quick detour to splitting and merging. Splitting takes one treap and produces two, a left treap and a right treap, where the left treap contains the values less than a given key and the right treap contains the values greater than a given key. We assume that the key is not in the treap.3 [3 Otherwise, which output would it go in?] Of course, the left and right treaps that result from the splitting must themselves be valid treaps.
To do that, we're gonna cheat. First, we add in a new node with the
given key, but give it a really low priority (I'm going with -1) so
that it becomes the root. Then we can just pluck off left and right
subtreaps and return those. Nice and simple, huh?
(def split (key root)
(let (ins (set key #0 root #:(p (- 1))))
(pair ins.left ins.right)))
Because insertion is functional, we never have to explicitly remove the dummy node.
The opposite of splitting is merging. Merging takes two treaps that
might have been the result of a split, and merges them into one treap.
How can we implement that? Well, the root element of the new treap
must be the root of one of the two treaps—whichever has the lowest
priority. Let's say it's the root of the right treap; in that case,
the new root's right child must be the right treap's right child,
since that already contains all the nodes larger than the new root.
Meanwhile, the left child must be the merger of the left treap and the
right treap's left child.4 [4 The #t below is the pylisp syntax for
the true boolean, so it's the default clause of the conditional.]
(def merge (left right)
(cond
((not left)
right)
((not right)
left)
((< left.p right.p)
(Node left.p left.key left.val left.left (merge left.right right)))
(#t
(Node right.p right.key right.val (merge right.left left) right.right))))
Note
The first time I wrote this, there were errors. They are now fixed. The new code is deceptively similar; but then again, even minor changes are crucial in recursive functions, since those errors propogate.
Deletion
Deletion is the grave yard of balanced binary trees—for red-black trees, Wikipedia lists six cases. But deletion for treaps is very nice and intuitive. Intuitive!
Consider the node you want to delete. If your node is a leaf node, just delete it. If it has one child, remove the node and replace it by its child. And if the node has two children? Then, when you remove it, merge its two subtreaps into a replacement:
(def del (key root) (cond ((not root) (signal '(error not-found key del) key)) ((< key root.key) (Node root.p root.key root.val (del key root.left) root.right)) ((> key root.key) (Node root.p root.key root.val root.left (del key root.right))) ((= key root.key) (merge root.left root.right))))
But we can do even simpler:
(def del (key root)
(let (halves (split key root))
(merge (car halves) (cdr halves))))
Note the pure, happy simplicity of this method! Oh, the joys of treaps!
Usage
I like to add some test code to the bottom of my files. Not exhaustive unit tests,5 [5 We don't want import taking forever, do we?] but a quick sanity test, just to make sure everything works. Let's do that here:
(use tester) (test "Sanity check" (let (treap #0) (set! treap (set 5 'a treap)) (set! treap (set 7 'b treap)) (assert (= (get 5 treap) 'a)) (assert (= (get 7 treap) 'b)) (set! treap (set 2 'c treap)) (assert (= (get 2 treap) 'c)) (set! treap (set 2 'd treap)) (assert (= (get 2 treap) 'd)) (set! treap (del 5 treap)) (assert (not (in 5 treap)))))
That checks that the treap works. But is it balanced?
(test "Fairly Balanced" (let (treap #0) (signal '(warning test slow-test) "Balancing test") (for (i (range 1000)) (set! treap (set i #0 treap)) (print i)) (assert (< (depth treap) 40))))
Wrapping up
Overall, this code weighs in under 100 lines, and if that's not impressive, go implement red-black trees. We'll see who's laughing.
What about cool optimizations? Anything in that department? Well, it's a good thing you ask. There're all these priorities floating around. Don't you just get the urge to fiddle with them?
One simple optimization would decrease the priority of a node every
time it is accessed (whether by get or set). This will slowly migrate
your commonly-accessed nodes up to the top of the treap, where they're
faster to get at. But this can slow down accesses, because you'd need
to rewrite the treap.
I'm not providing code for this variant, because it's not worth it in
my experience. If you have a treap of several thousand elements but
you only ever access three of them, you're doing something else wrong.
If you do implement it,make sure split deals with non-unique
priorities correctly. But as always, look before you leap, benchmark
when in doubt, beware of dog.
A quick problem
Suppose we want to create a sorted array; that is, we want to be able to retrieve the $n$-th largest key, in \(O(\log n)\) time. Treaps (or, really, any balanced binary tree) provide a nice way to do this. As a hint, consider the fact that we're not using the value stored in each node for anything, thus leaving it open to be appropriated for some purpose.
Acknowledgments
Thanks to Sam Fingeret for first introducing me to treaps, and for helping out with the details of the proof that the height is expected to be logarithmic. Thank you as well to Mark Velednitsky for editing this writeup, even though he can't stand the sight of Lisp. I also edited the page in 2019 to make it 20% shorter. I hope you find the results short but clear.
Thanks also to folks on Hacker News who provided a lively discussion, and to Patrick Stein who did an implementation in Common Lisp.
Footnotes:
I'm ignoring duplicate keys, but they don't change much.
Note that #0, the null object, is my representation of
the null treap.
Otherwise, which output would it go in?
The #t below is the pylisp syntax for
the true boolean, so it's the default clause of the conditional.
We don't want import taking forever, do we?
