MegaLibm: a Math Library Workbench

To make this concrete, let's work through how to built an asin(x) implementation similar to (a bit better than) the one above. We'll use the following algorithmic choices.

• asin(x) is an odd function, so negative inputs and positive inputs work in symmetric ways
• Since asin(x) = pi/2 - 2 asin(sqrt((1 - x) / 2)), reduce inputs in [0.5, 1] to the domain [0, 0.5]
• You can use a polynomial to approximate asin on [0, 0.5]
• Since asin is odd, the polynomial should only use odd terms
• Evaluate the polynomial in two-wide Estrin form so it can be vectorized a bit
• If you fix the first term of the polynomial to 1.0, you save a multiply

There are more tricks you might use, but this is representative. Let's look at what the MegaLibm implementation of this looks like. Since asin(x) is odd, we know that if we negate inputs in [-1, 0], evaluate asin on the reflected input, and negate the output, we'll get the right answer. Since this is a common operation, MegaLibm has a FlipLeft operation for that:

FlipLeft([-1, 0], -x, -y, ...)

Here FlipLeft indicates that inputs in [-1, 0] should be mapped to [0, 1]; that the mapping should negate the input (-x) and then negate the output back (-y). Note that -x and -y are symbolic expressions here, they don't evaluate to numbers.² [² These arguments always using the variables x for inputs and y for outputs; MegaLibm currently only support single-argument functions.] Finally the ... is where the implementation of asin on [0, 1] should go. That implementation can flip inputs in [0.5, 1] to inputs in [0, 0.5] using that crazy identity:

FlipRight([0.5, 1], sqrt((1 - x) / 2), pi/2 - 2 * y, ...)

Here the mapping functions are more complex, but it's basically the same concept. Now, we need a polynomial approximation. In MegaLibm, that's split into two steps. First, how to generate the polynomial itself:

Polynomial([0.5, 1], asin(x),
  powers=[1, 3, 5, 7, 9],
  coeffs=[1, ..., ..., ..., ..., ...])

Here we're saying that we want to use a polynomial approximation to asin(x) on [0.5, 1] using odd powers and fixing the first coefficient at 1. For the other coefficients, I've written ...; you'd fill those in with floating-point numbers derived from a tool like Sollya.

Finally, now that we have a polynomial, we can evaluate it:

EstrinForm(Polynomial(...), split_first=True, width=2)

The EstrinForm built-in evaluates polynomials using Estrin form (here using width 2) and is smart enough to notice that, since the polynomial only has odd terms, it should be evaluated as a polynomial in x^2. The split_first indicates that the first term of the polynomial should be split out; the MegaLibm simplifier can then notice that the first term is 1 and save the multiply.

Now, if you haven't designed math functions before, these steps may feel pretty mystifying—how do people come up with that? For now, please take my word for it that they somehow do. And moreover, with MegaLibm you can rapidly prototype implementations and test out the effects, because any MegaLibm implementation can be automatically compiled to C and run to test performance or accuracy. For example, it's pretty easy to test the differences between Horner form and Estrin form, or test several different Estrin widths to tune your implementation.

And there are lots of other implementation options available in MegaLibm. For example, if you want to use double-double tricks in your polynomial—that's an optional parameter for EstrinForm. If you want to handle edge cases specially, or maybe carefully round the endpoints inward—that's available. If you want to handle inputs near 0 with a fast path—sure. And if there are tricks we don't know about, those could be added to MegaLibm.

Now, imagine how many mistakes you could accidentally make while writing an implementation like this. Is that complicated identity actually true? Does it actually map inputs in [0.5, 1] to inputs in [0, 0.5]? Should the first coefficient be 1 or -1? It's so easy to miss a sign, or a factor of two, or make some other mathematical mistake. Luckily, MegaLibm has a type system that can automatically catch most such errors.

There are two key types in MegaLibm: mathematical functions and function implementations. A mathematical function Function<x> is represented by symbolic expression in x, while a function implementation is a type Impl<f, [a, b]> where f is the Function<x> being implemented and [a, b] is the domain it is implemented on. (There are also auxiliary types like real numbers, floating-point numbers, polynomials, lists, and so on.) Most of the operators shown above operate on Impl terms; for example, FlipLeft takes in an Impl and produces an Impl; EstrinForm takes in an auxiliary type called Polynomial<f, [a, b]> but it returns an Impl.

But, importantly, type rules in MegaLibm can include both type checks as well as mathematical side conditions. For example, the rule for FlipLeft looks like this:

a, b : Real
reduce : Function<x>
reconstruct : Function<y>
e : Impl<f, [b, 2b - a]>

forall x in [a, b], reduce(x) in [b, 2b - a]
forall x in [a, b], reconstruct(f(reduce(x))) = f(x)
-------------------------------------------------------------------------
FlipLeft([a, b], reduce, reconstruct, e) : Impl<f, [a, 2b - a]>

To walk through these, we first have normal type judgments for a, b, reduce, and reconstruct, plus e. In the type judgment for e, note that the domain changes, because inputs in [a, b] are being mapped into the range [b, 2b - a]. (There are more variants of Flip where the domains can be split somewhere other than the midpoint.)

Then, after the normal type judgments, there are some forall-quantified mathematical identities that must be true. These are automatically checked by MegaLibm, either using a built-in e-graph based solver or by calling out to Mathematica (or, if neither works and you allow it, sampling). This ensures that you got all your signs right, and that any identities you used are true.

This mitigates a lot of the risk of prototyping, testing, and tuning library implementations and, more subjectively, totally changes the experience. Instead of implementation writing happening mostly on paper and most of the brain-power going to mathematical proofs, everything now happens mostly on the computer, interactively, with the computer doing all of the checking and the implementor being free to think about higher-level concerns like accuracy and speed.

Also, the fact that MegaLibm has a large built-in library of implementation tricks makes it easy to discover new approaches, and the fact that MegaLibm will automatically handle the tricky (Cody-Waite reductions), error-prone (double-double tricks), and nit-picky (higher-precision constant evaluation) aspects of implementation takes a lot of the tedium out of the process.

Finally the MegaLibm code serves as a kind of documentation—most math implementations out there have something like an English algorithmic description embedded as a large comment at the top of the file. The MegaLibm code replaces that while being more precise, machine-readable, and easy to edit or tune later.

One place the expertise is really necessary is using the coterie of tools that handle various aspects of math library implementation. For example, to derive polynomial coefficients, you usually want to use the Remez algorithm, available from a couple of specialized math systems like Mathematica or Sollya. And interacting with these tools requires experience of its own—the tools need to be installed on one's machine (already not easy!), the input language learned (often quite complex), error messages understood and corrected (often requiring mathematical insight), and finally the outputs correctly transcribed back into the source code.

Luckily, MegaLibm's typed DSL simplifies most of these interactions. For example, take the example above, where I wrote ... for the polynomial coefficient. That's MegaLibm syntax for a hole.³ [³ MegaLibm is embedded in Python, where this is valid syntax, odd though it may look.] Since MegaLibm is typed, it knows that this hole needs to be filled with real number coefficients, and it can interface with Sollya to do so:

impl = FlipLeft(...)
impl.fit()

The fit method searches the polynomial for holes inside a Polynomial term (if the function and interval are concrete), translates the function and interval into a Sollya query, waits for Sollya's answer, and then returns a new implementation with the holes filled. The fit method has loads of optional arguments to configure the fit algorithm (remez or fpminimax), the accuracy goal (relative or absolute error, or something even more complex), working precision (and other nit-picky options), and even the external tool to use (if you prefer, say, Mathematica's MiniMaxApproximation).

The implementor would issue this call in a Jupyter notebook and (after waiting a bit) see the hole-filled implementation printed to their screen, where they could examine it and copy the coefficients if they liked the results. If they don't need to see the coefficients, they could just use impl.fit() directly in further steps:

impl.fit().measure_error()

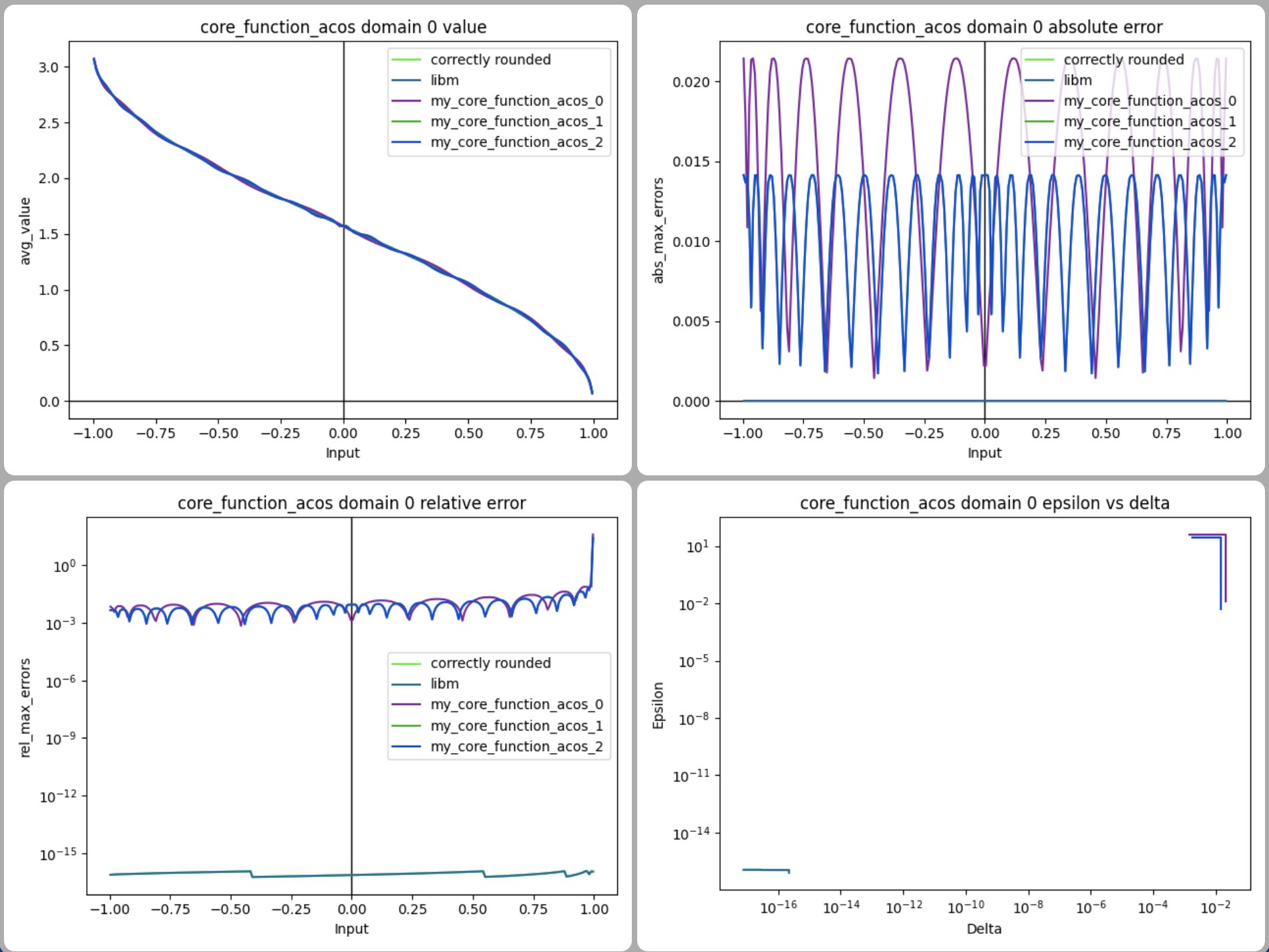
Here, while the measure_error estimates the error of the implementation (using sampling with MPFR for lower bounds or FPTaylor with Gelpia for upper bounds, or both) and visualizes the error in a plot like this one:⁴ [⁴ This is from an in-progress version of the tool and actually visualizes three different implementations of acos, with the GLibC and CRLibm versions for reference.]

Similarly, to measure performance, the implementer can compile their implementation to C and run it:

impl.fit().compile().measure_speed()

The compile command compiles the implementation to C, configurable with optional parameters both for the compilation (vectorize?) and the C compiler (-mtune=native?), and then the measure_speed command generates random inputs and measures how long the implementation runs on them (again, the distribution of inputs is configurable, as are options like trashing the CPU cache every so often to estimate the impacts of latency).

Not only does this abstract over the tedious steps like managing files, running the C compiler, and setting up driver code, but it also makes it possible to integrate measurement into the design and tuning loop. The notebook interface facilitates rapid exploration, visualizes data with plots, and also handles saving the results of each step for later tuning. The notebook becomes documentation that can be saved and committed to the same source code repository as the compiled implementation, or even potentially rerun in CI to ensure that, say, an accuracy or performance bound is reached.

The point isn't just that MegaLibm has a bunch of useful tools built in, but that the MegaLibm DSL provides an easy way to integrate tools. MegaLibm's types and its careful split between the math and the implementation provides plenty of context for tools to leverage, and the notebook interface provides an integrated space for both implementation and testing. I think it would be straightforward to extend MegaLibm with tricks like rational approximation and tools like Maple to help users use those tricks. Or with a deeper understanding of mixed-precision computation and then also integrate a tool like FPTuner to automatically generate precision annotations. Breakthroughs like RLibm could be plugged into MegaLibm and then immediately tested and used by library implementors.

For example, we might try to integrate accuracy and performance debugging tools into MegaLibm. We haven't implemented these yet, but it would be great if, after a measure_error call, the implementation could be printed with each step annotated with its local error (estimated from samples or FPTaylor). Likewise, we could probably compile in calls to CPU performance counters and print an implementation annotated with the performance impact of each algorithmic decision.

Imagine that you are not a numerical methods expert. (Who among us can really claim that title, anyway?) Then you likely wouldn't be able to write the example implementation above—certainly not without help. Instead you can start with a very general implementation:

impl = Impl(asin(x), [-1, 1]).hole()

This method, ImplType.hole, generates an implementation containing just a hole. (You can't write it ... because MegaLibm needs to know the type.) Of course, this implementation isn't very useful on its own—you can't run it, or measure its error, or anything like that—but MegaLibm tools can be used to help complete it. For example, you can run:

impl.synthesize_flips().synthesize_polynomials()

This directs MegaLibm to first attempt to synthesize FlipLeft and FlipRight terms, and then fill the remaining holes with polynomial approximations. Just like with fit above, it then prints the resulting implementation.

For asin, it's smart enough to automatically discover that asin is odd and therefore that a FlipLeft can be used for the negative half the range. Similarly, because asin is odd, the synthesize_polynomials step will only use odd powers. For more-expert users, the synthesize_flips step is configurable with hints, while the synthesize_polynomials step is configurable with how many powers to use or how to attempt to synthesize the coefficients. Less-expert users can skip even the detail of flips and polynomials using the generic synthesis command, which synthesizes periodicity, flips, and polynomials.

The synthesis is basically a type-directed synthesis. For each hole, it considers all MegaLibm constructs one by one, checks whether the types match, and if they do attempts to prove the necessary side conditions (like identities) or compute the necessary parameters (like the period of a periodic function). This again shows how useful the MegaLibm type system is for integrating tools. To discover identities, MegaLibm uses e-graphs in a really clever way (details one day in a paper) to find interesting mathematical identities of the function you're implementing. Along the way, it uses e-graphs for generating candidate identities, for proving equality, for simplification, and even for solving inductive equations.

Now, the synthesis isn't magic. It's not smart enough to discover that crazy asin identity used in the example, but I think more careful work on rewrite rules, e-graph algorithms, or similar could get us there. And if MegaLibm's synthesis engine doesn't find some rewrite, an expert can always build that implementation by modifying the synthesized output.⁵ [⁵ MegaLibm provides a NamedHole construct to make that kind of plugging and replacement easy.] And the synthesizer can run for minutes, so it's not as breezy an experience as one would like.⁶ [⁶ Though I have high hopes that the e-graph engineers on the egg enterprise will invent new ways to speed up the synthesis.]

But even simple synthesized implementations have a lot of value. In simple cases like sin, MegaLibm's synthesizer gives decent results, and because it knows about sophisticated techniques like Cody-Waite reduction the synthesized implementations, while not as good as expert-written ones, can have acceptable accuracy and speed. And for users who haven't studied math library implementation (like students in my classes) seeing a few examples can give them a lot more confidence to explore further.

And the interactive notebook interface itself makes synthesis much more useful. While it's not obvious above, the synthesize steps return something called a ImplSet, which has a filter helper method for selecting the implementations with the best accuracy of performance. For example,

implset = impl.synthesize()
implset.filter(Impl.measure_error, Impl.measure_speed).all()

measures the error and speed of each implementation and throws away any implementations that aren't Pareto-optimal, returning a much smaller list than simply impl.synthesize().all(). Implementers can also use ImplSet directly if it's helpful, constructing multiple implementations and then identifying the best to use on a particular machine.