Zippers, Part 1: Huet Zippers
A zipper is a purely functional cursor into a data structure. The cursor can be moved around the data structure, and parts of the data structure close to the cursor can be updated quickly. This first of four parts discusses zippers as an explicit data structure pattern, as described by G. Huet. Huet didn't discover or invent zippers; instead, his paper (PDF) discusses the algorithm as something well known in the programming "folklore". Huet was, however, the first to publish the zipper, and so it is named after him. Let's explore his construction.
Updating a List
def/adt (List ,a) [
Cons ,a (List ,a)
Nil ]
Now, it's pretty easy to write a function to "update" a list in a purely functional way:
def/fns list-set <-
; Base case
[(Cons fst rest) 0 new-val] <-
return (Cons new-val rest)
; Inductive case
[(Cons fst rest) pos new-val] <-
let (new-rest <- list-set rest (- pos 1) new-val) <-
return (Cons fst new-rest)
Note that this function is expensive mostly due to the fact that is must constantly allocate new list nodes. But in fact, most of this allocation is useless. If we set two values, we end up allocating new nodes to keep around the version of the code between changing the first and second position.
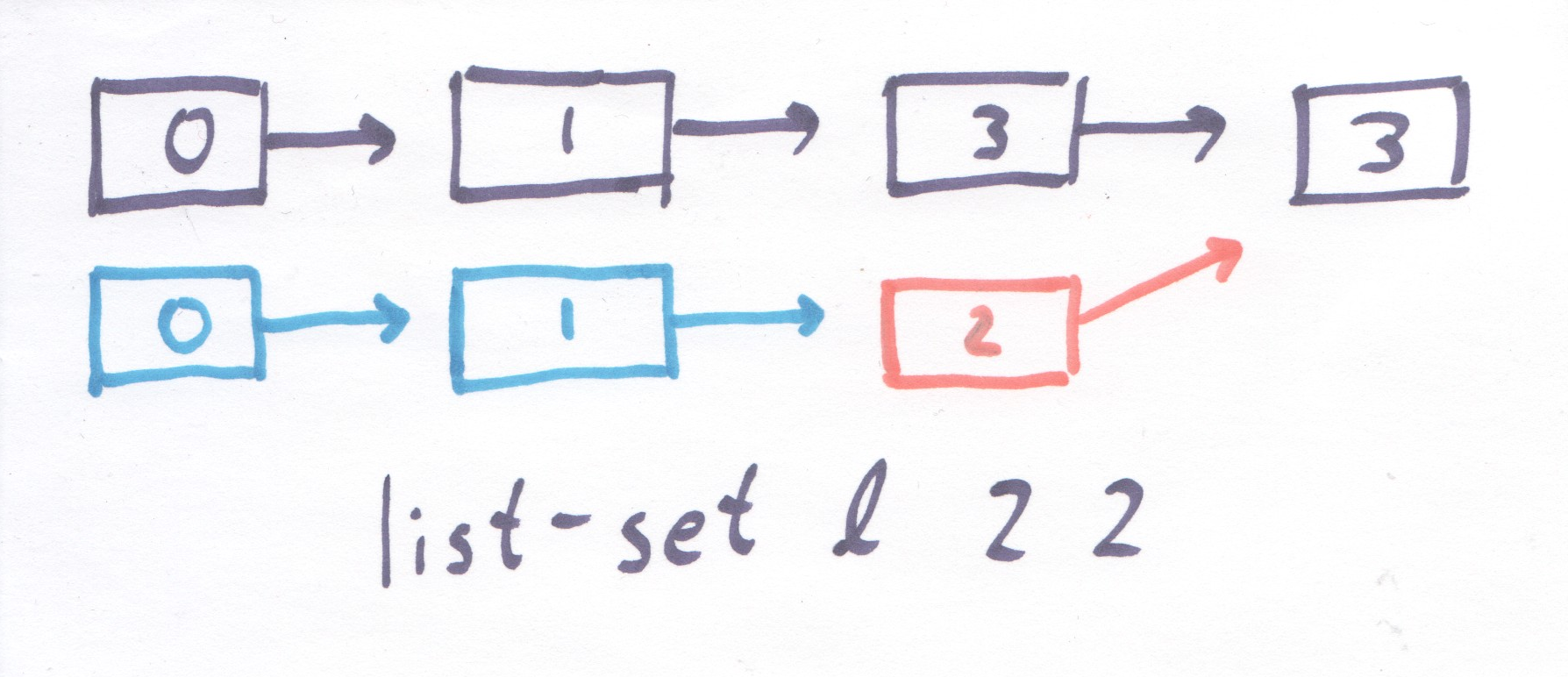
Figure 1: Lots of useless allocation
It also wastes time if we use it a lot on the same list, since we have to constantly crawl to find the right position in the list, then crawl back recreating new nodes. If we are making several close-by changes, this is very wasteful! After all, we are crawling back and forth across the same region of the list over and over again.
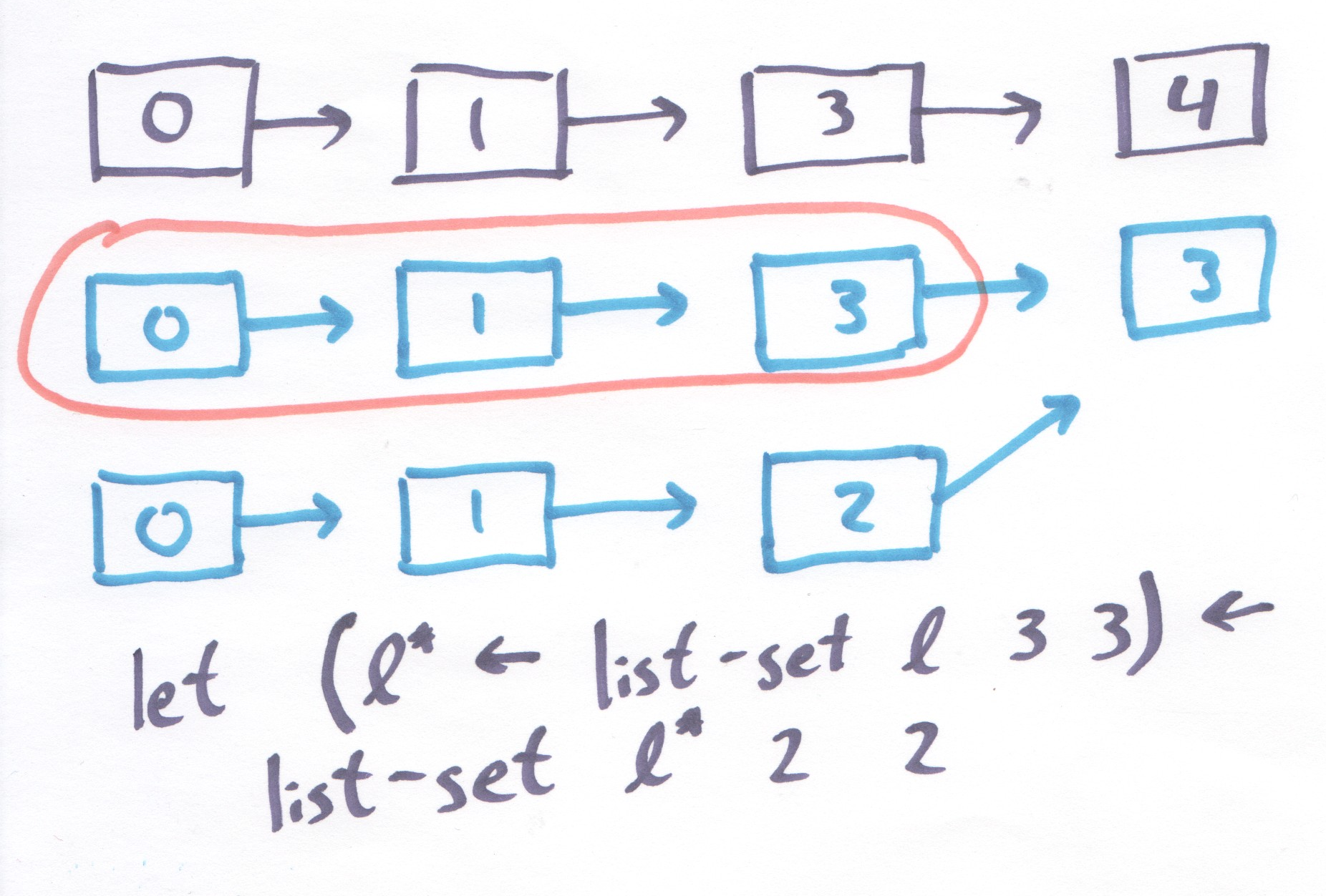
Figure 2: How wasteful!
It would be better if we could crawl forward along the list to a certain point, and then make multiple updates to the list before crawling back and allocating new nodes. This is precisely what the zipper achieves.
Focusing on Cursors
The Huet zipper is born by focusing on where exactly this "cursor" currently is — where in the structure we can cheaply modify nodes, and where we can move this location to. To do this, instead of keeping the data linked in the normal way, we always make sure all of our pointers away from the cursor.

Figure 3: A list with a Huet zipper
To actually implement this, we'd see that we effectively have two lists, a forward list and a backward list:

Figure 4: A forward and a backward list
Using this model, we can implement moving forward or backward through the list and updating the value at the cursor:
def/adt (ZList ,a) [
ZList (List ,a) (List ,a) ]
def/fn ZList:left ((ZList (Cons lhead lrest) rlist)) <-
ZList lrest (Cons lhead rlist)
def/fn ZList:right ((ZList llist (Cons rhead rrest))) <-
ZList (Cons rhead llist) rrest
def/fn ZList:set ((ZList llist (Cons rhead rrest)) new-val) <-
ZList llist (Cons new-val rrest)
Now, multiple operations to the same area of the list only require a
small bit of crawling along the list and relatively few allocations.
In fact, every individual zipper list (zlist) operation takes
constant time and constant allocations. So long as we don't need to
move the cursor too much, this gives us significant gains over the
naive method of updating lists.
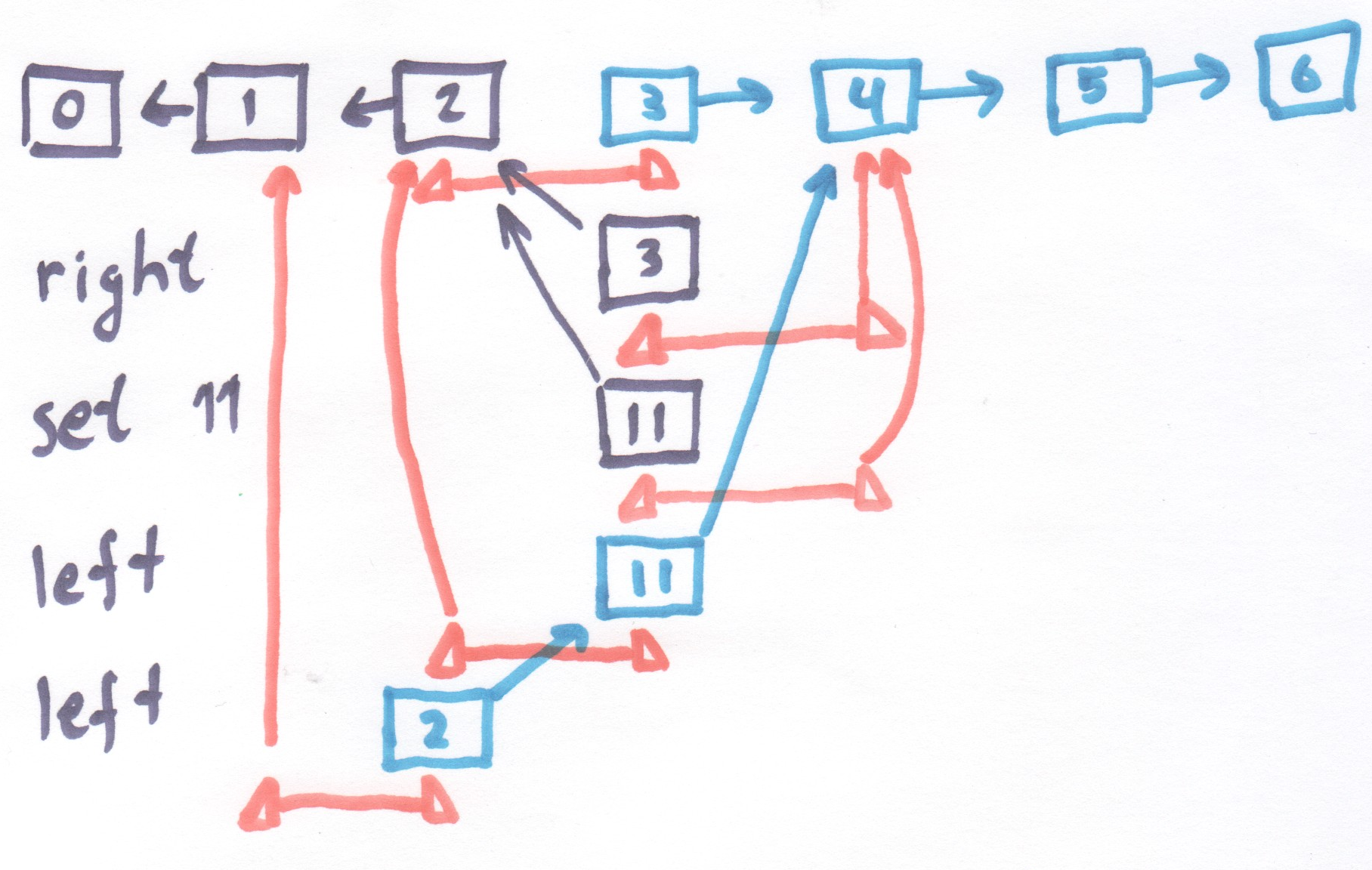
Figure 5: Every individual operation requires only one allocation
Extending Zippers to Trees
A list is a pretty simple data structure. More complex is a tree, so let's talk about how we might extend zipper operations to work on, say, a binary tree.
A binary tree is defined similar to a tree, except that each internal node has two children:
def/adt (Tree ,a) [
Node ,a (Tree ,a) (Tree ,a)
Empty ]
As for a list, it's pretty easy to write a naive update function, say one that takes a path and a new value:
def/adt Direction [L R]
def/fns tree-set <-
; Base case
[(Node val ltree rtree) [] new-val] <-
Node new-val ltree rtree
; Path starts with Left
[(Node val ltree rtree) [Left & rest] new-val] <-
Node val (tree-set ltree rest new-val) rtree
; Path starts with Right
[(Node val ltree rtree) [Right & rest] new-val] <-
Node val ltree (tree-set rtree rest new-val)
And as for a list, this function results in needless allocation:
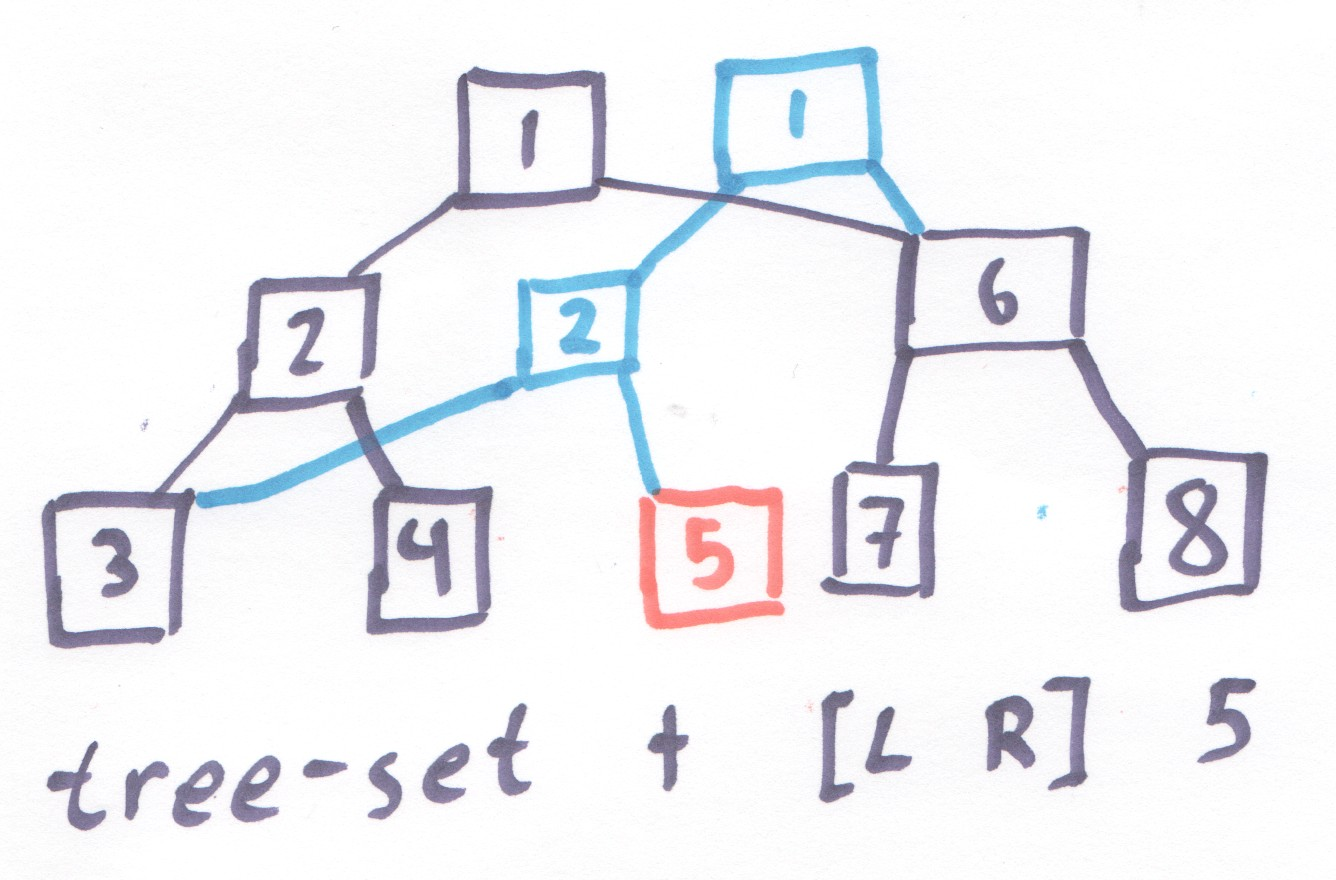
Figure 6: As with lists, there is unneeded allocation here
To adapt the zipper to this more complex structure, we remind ourselves that the core idea is to track where the cursor is and how it can move. So to get a zipper, we again just have to point all pointers away from the cursor:
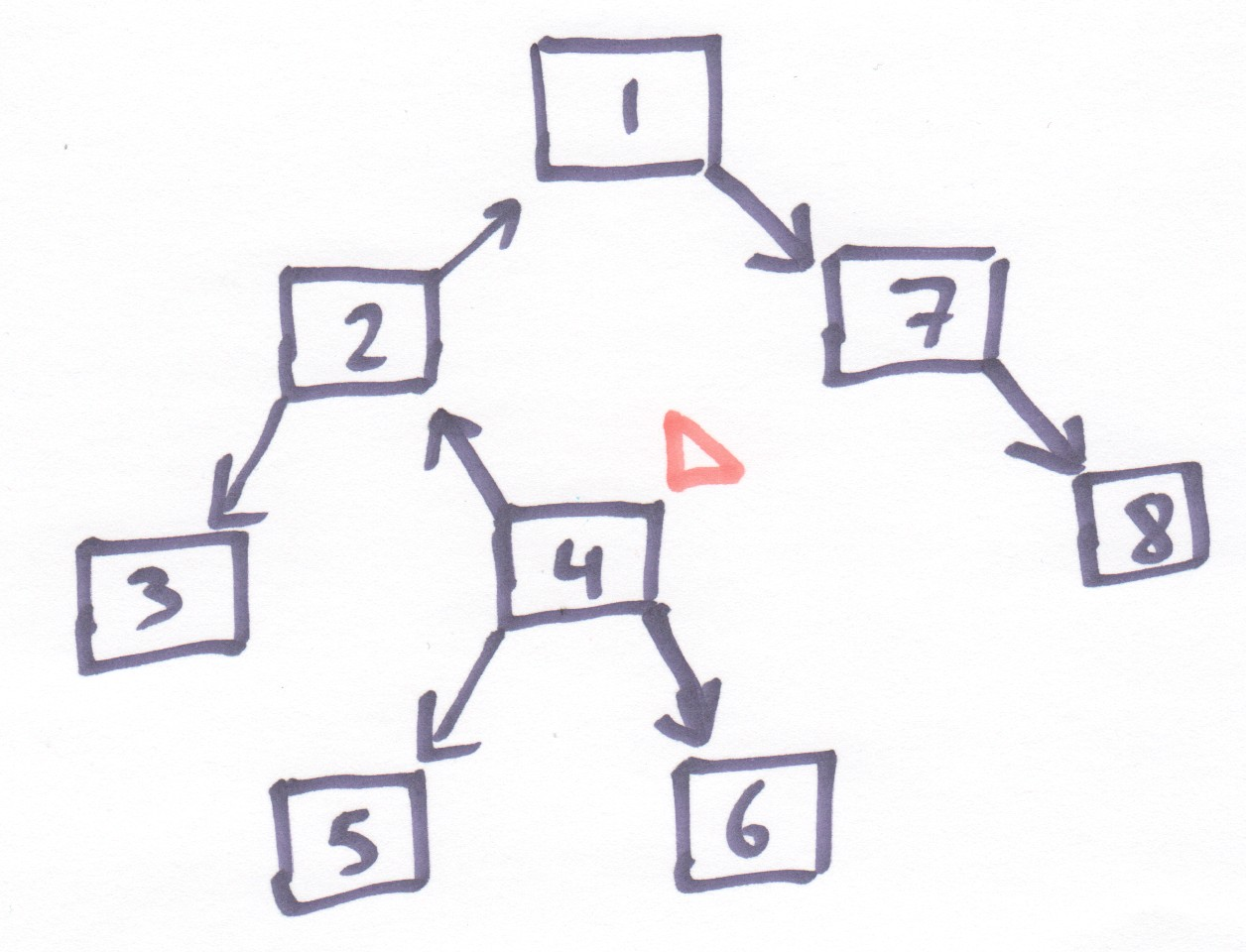
Figure 7: A tree with a cursor somwhere in the middle of it
It might not be quite obvious how to implement this structure at first glance. However, if you look closely, you'll note that there are really two parts to this tree-with-odd-pointers: there the pointers that were reversed, which form a list going up to the root; and there are the things hanging off of that list, which are normal trees:
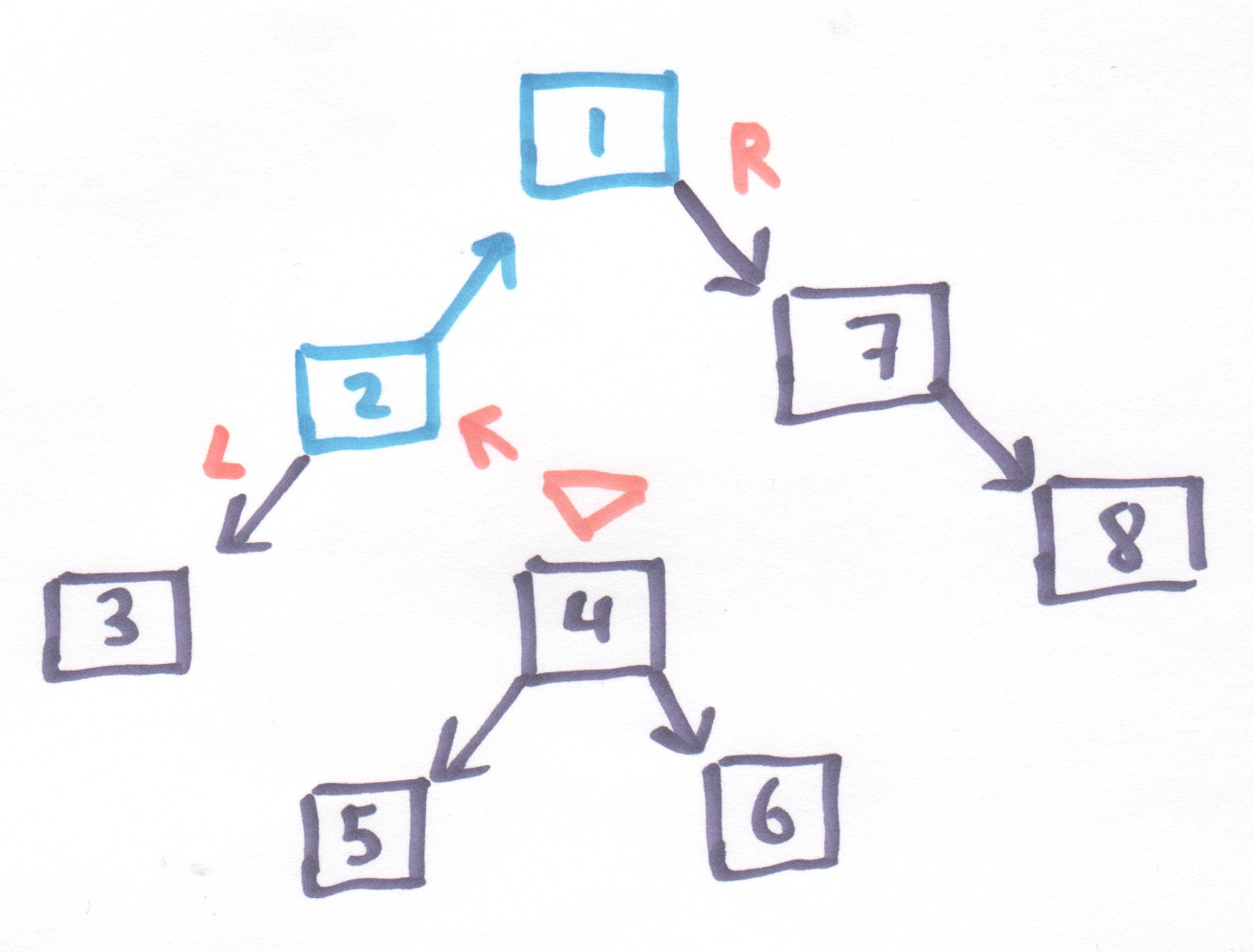
Figure 8: A tree with a zipper is really a list of trees
But note that we also have to keep track of which direction each of the trees hanging off our list of "breadcrumbs" is supposed to stick out in.
Now, we can again implement the basic operations for our cursor, ensuring that all of them are constant-time and constant-allocation.
def/adt (ZTree ,a) [
ZTree (List (Tuple ,a Direction (Tree ,a))) (Tree ,a) ]
def/fn ZTree:left [(ZTree bread (Node val ltree rtree))] <-
ZTree [(Tuple val L rtree) & bread] ltree
def/fn ZTree:right [(ZTree bread (Node val ltree rtree))] <-
ZTree [(Tuple val R ltree) & bread] rtree
def/fns ZTree:up <-
; Were to the left
[(ZTree [(Tuple val L rtree) & bread] subtree)] <-
ZTree bread (Node val subtree rtree)
; Were to the right
[(ZTree [(Tuple val R ltree) & bread] subtree)] <-
ZTree bread (Node val ltree subtree)
def/fn ZTree:set [(ZTree bread (Node val ltree rtree)) new-val] <-
ZTree bread (Node new-val ltree rtree)
A picture for this case would be too confusing. But it's easy to verify that each function takes constant time, since each just does a single allocation.
So What Have we Got?
So, having done all of this work, what are our results? Well, we have a new data structure that allows us to quickly make changes to a structure, in a purely-functional way. Furthermore, we can easily see that this data structure improves localized changes to take \(O(1)\), not \(O(\lg n)\), time.
So we now have a spiffy new data structure that allows basic operations on a data set quickly and elegantly1 [1 As an example to real-world use, I point you to XMonad, which uses zippers to track which window is focused.]. However, while the overall idea of zippers is hopefully clear, it's not obvious how to easily write a zipper for any old data structure. For that, we need to consult some theory. But that's for part 2…
Footnotes:
As an example to real-world use, I point you to XMonad, which uses zippers to track which window is focused.
