Pavel Panchekha

By Pavel Panchekha, Jeffrey Prouty

Share under CC-BY-SA.

Problem Set 15 (Given 03/25/12)

Level I

  1. A circuit contains a \(1 V\) battery, a \(5 \Ohm\) resistor, and a \(1 \mu F\) capacitor. How long would it take to charge the capacitor to half-full? Three-quarters-full? 99% full?

  2. The space between two plates of a parallel-plate capacitor is divided into four parts, as in the figure below, and the parts filled with different dielectrics. Find the capacitance of this capacitor, if with no dielectrics it would have had capacitance \(1 \mu F\).

    15-2.png

    Figure 1: Figure for problem 2: find the equivalent capacitance.

  3. A circuit containing an initially charged capacitor, and inductor, and a resistor is set up, and it is determined that the current in the circuit oscillates with time but eventually dies out. Explain qualitatively why this happens. Why does the current oscillate, why does it eventually die out?

Level II

  1. Verify with a differential equation the rule for capacitors in parallel.

  2. The below circuit is set up, and the switch connected at time \(t=0\). Describe the initial voltages and currents at every point of the circuit, and the voltages and currents after a long time has passed. What is the eventual charge on the capacitor?

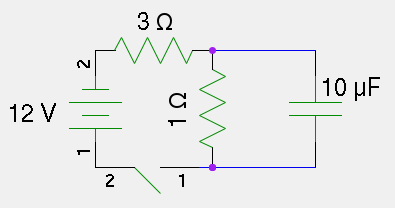
    15-5.png

    Figure 2: Figure for problem 5: describe this circuit

  3. How much work is required to (very quickly) insert a dielectric with constant \(k\) into a capacitor when it is half-charged? When it is fully-charged?

Level III

  1. Solve for the transient behavior of the circuit in Problem 5; that is, find the charge on the capacitor as a function of time. Use the same approach we used to derive the equations for RC circuits to derive the equations for this circuit. As a hint, set up all of the equations in terms of the charge \(Q(t)\) on the capacitor (you'll need to represent various currents in terms of this amount), which will give you a differential equation. The differential equation is separable with a bit of ingenuity, so separate it and rearrange nicely.
  2. Imagine you have a setup similar to that of problem 2, but instead of having four regions of differing dielectric coefficient, all of the space between the two plates is made up of differing dielectric coefficients. Imagine a function \(k(x, y, z)\) giving the dielectric coefficient of a tiny box around \((x, y, z)\). Find the effective dielectric coefficient of this aggregate dielectric. As a hint, consider that parallel capacitors simply add capacitances, so the problem can be broken up into a surface integral of a particular function. Then determine how to find that function with another integral. It isn't necessary to simplify beyond that point.
  3. Analyze an RLC circuit without a battery (the capacitor starts charged). It is not too difficult if you know how to solve the necessary differential equation. The trick is to imagine that the solution is of the form \(Q(t) = e^{\lambda t}\). Substituting this in will reveal several viable values of \(\lambda\); the solution to the differential equation has the form \(A e^{\lambda_1 t} + B e^{\lambda_2 t}\) if \(\lambda_1\) and \(\lambda_2\) are distinct.