Problem Set 14 (Given 02/26/12)

Level I

You have a small magnet, oriented with the north pole in the \(+{\hat z}\) direction and with the south pole in the \(-{\hat z}\) direction. You also have a circular loop of wire in the \(xy\) plane, centered at the \((0, 0, -d)\). You take the loop and move it along the \(z\) axis from \(-d\) to \(d\). Graph the current through the loop as a function of time. Then graph the power output as a function of time.
You attach a DC electric generator to a DC electric motor, such that the motor rotates the flywheel of the generator (so if the job of the motor is to rotate an axis, it rotates the axis whose rotation produces power in the generator). Describe at least 3 ways in which energy escapes this system, causing this system to eventually lose power.
If you take a small magnet and move it toward a solenoid (recall: coil of wire), you will generate a large current in the solenoid. On the other hand, if you move the small magnet into the interior of the solenoid and move it around, you will generate almost no current at all. Why?
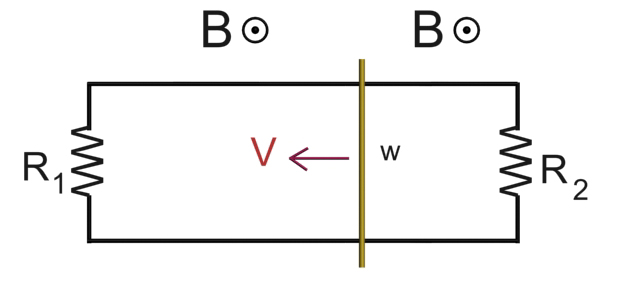
As in the image below, you have a rectangular loop of wire with two resistors in it, with resistances \(R_1\) and \(R_2\), and which has a conducting rod connecting two opposite wires. This rod moves with velocity \(v\). Find the current flowing through each resistor and the power lost as heat in each. Also find the force on the rod.

A rocket is attached by long conductive wires to the points \((0, 1)\) and \((1, 0)\), which are also connected by a wire, forming a triangular circuit. The rocket starts at point \((\frac12, \frac12)\) and can generate a force \(F\) along the line \(y = x\). Everything takes place in a magnetic field \(\mathbf{B} = B_0 {\hat z}\). You fire the rocket; write a differential equation describing its motion, as well as the initial conditions you would solve from.
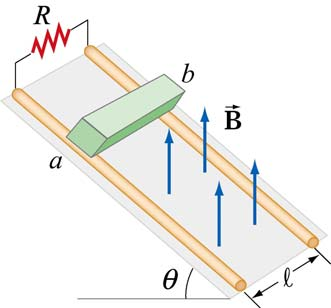
As in the image below, a conducting block of mass \(m\) slides down a ramp along conducting rails; the rails are joined at the top of the ramp by a resistor of resistance \(R\). There is a vertical magnetic field of magnitude \(B\). Graph the velocity of the conducting block and find the terminal velocity, if any.

Design a generator that produces power from linear motion. You can imagine having a person slide a handle like in a trombone. Your generator should produce DC current assuming that the person applies constant force (switching directions instantaneously).