Problem Set 10 (Given 01/22/12)
Level I
- The average home has a main power line carrying up to approximately 200 amps of current, at the standard 120 volts. How many 100-watt lightbulbs can that support? Electricity costs about 12 cents per kilowatt-hour. If I use all of the capacity my main power line can carry (that is, all 200 amps) at all times of day, how much does this cost me over the course of a year?
- A 1.5 volt battery is hooked up to a 10 watt lightbulb. What's the largest possible resistance of the lightbulb if it is at its full brightness? What is the corresponding current?
- Given three 2-ohm resistors and a 2-volt battery, what are the possible currents you can have running through the circuit (more particularly, the current you'd have leaving or entering the battery)?
- You have a $n$-gon of 1 Ω resistors. What is the equivalent resistance between two adjacent points?
Level II
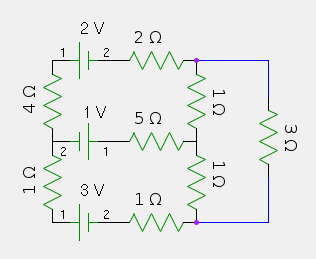
Solve the circuit below; that is, find the current at any point. What is the total power dissipated?
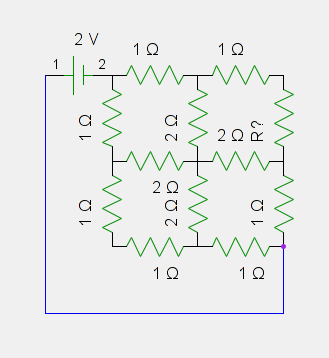
Solve the circuit below; that is, find the current at any point. If a the battery can power this circuit for an hour, how much energy does it store?
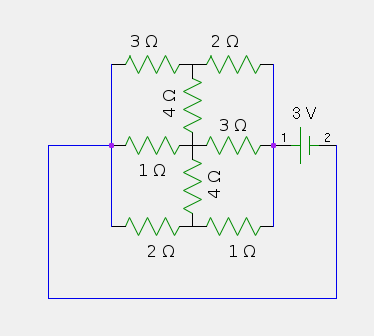
Solve the circuit below; that is, find the current at any point. Are any of the batteries being recharged?
Level III
- You have a cube of 1 Ω resistors (that is, each edge of the cube is such a resistor). What is the equivalent resistance between two opposite points on the cube?
- What is the equivalent resistance between opposite corners of an \(n \times n\) grid of resistors? (For example, problem 4 discussed a \(3 \times 3\) grid of resistors.) An \(n \times m\) grid?
